【Godot】マッチ3ゲームの実装サンプルと解説

Godot Engine Advent Celendar 2022 14日目

この記事はGodot Engine Advent Celendar 2022 14日目の記事となります。

Godot Engine で Match-three game (マッチ3ゲーム) のサンプルを作成したので紹介です。

プロジェクトファイルは GitHub からダウンロードできます。

https://github.com/syun77/gd_match3

マッチ3ゲームの実装サンプルの紹介

マッチ3ゲームとは

Match-three game (マッチ3ゲーム) とは、グリッド上に配置されたタイルを特定のルールで3つ並べると消えるパズルゲームです。

ここでは、マッチ3ゲームの始祖と呼ばれる Bejeweled を参考に作ります。

タイルマッチングゲームの要素と名称

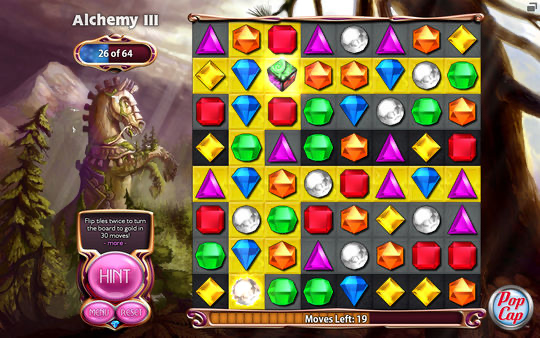
マッチ3ゲームは、タイルを一定の規則でならべて消す Tile-matching game (タイルマッチングゲーム) のサブジャンルです。この記事内で使用する用語は以下のとおりです。

マッチ3ゲームの構成要素

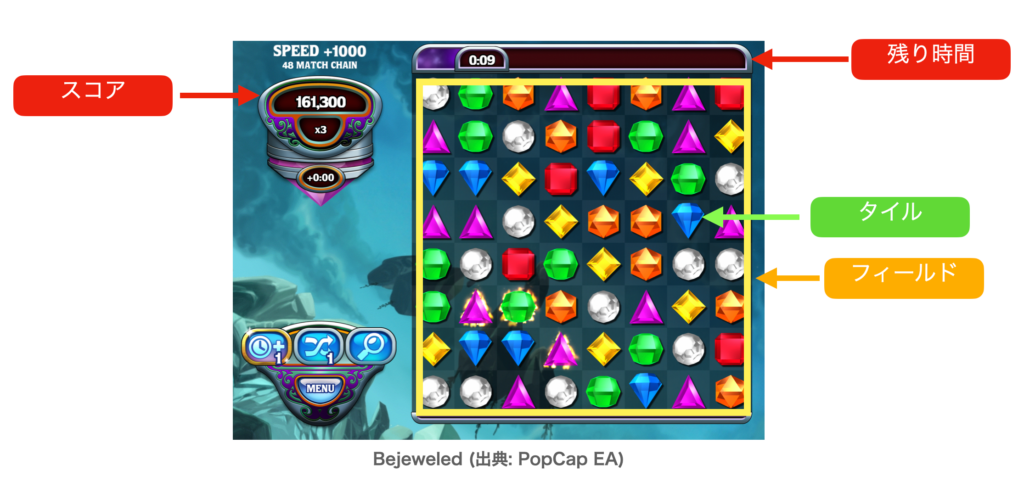
マッチ3ゲームを構成する要素としては、おおよそ以下のとおりです。

タイル（宝石）オブジェクト
タイルを管理するオブジェクト
選択カーソル
残り時間ゲージ
スコア（数値。文字列）

まずはプレイヤーが操作する対象である「タイル（宝石）」です。マッチ3ゲームでは、この「タイル」がグリッド（格子状）に並べられます。

また、そのタイルを管理するオブジェクトが必要となります。これはタイルの位置や消去判定、タイルの出現を管理するなど、目に見えるオブジェクトではないですが、マッチ3ゲームでのコアメカニクスを処理します。

そして「選択カーソル」です。マッチ3ゲームは、動かす対象となるタイルを選択してから移動します。そのためカーソルを表示して何を選択しているのかをわかりやすくします（下の動画では「黄色の宝石」をクリックしたときに、カーソルとして四角の枠を表示しています）

それ以外の「残り時間ゲージ」と「スコア」はゲームデザイン上重要な要素ですが、マッチ3ゲームを実装するためのコアな要素でないので、今回のサンプルでは割愛しています。

プロジェクトに含まれるデータの概要

このプロジェクトに含まれるデータの概要は以下のとおりです。

データの概要

res://
 +-- assets
 |    +-- tiles/*.png: タイル画像 (宝石画像)
 |    +-- cursor.png: カーソル画像
 |
 +-- Array2.gd: 2次元配列クラスのスクリプト
 +-- default_env.tres: デフォルト環境データ
 +-- FieldMgr.gd: タイル管理のスクリプト
 +-- FieldMgr.tscn: タイル管理シーン
 +-- font_theme.tres: 日本語フォントのテーマ
 +-- icon.png: Godotくん画像
 +-- Main.gd: メインシーンのスクリプト
 +-- Main.tscn: メインシーン
 +-- mplus-1c-regular.ttf: 日本語フォント(M+)
 +-- Point2.gd: 2次元座標クラス
 +-- Tile.gd: タイルのスクリプト
 +-- Tile.tscn: タイルシーン

データの簡単な説明

ゲームを開始したときのエントリポイントとして、Mainシーン (Main.tscn) が起動します。そして Mainシーンが フィールド管理シーン (FieldMgr.tscn) を呼び出して、フィールド管理がタイル (Tile.tscn) を生成する、という流れとなります。

そのほかに、Point2クラス と Array2クラスが存在しますが、これらはフィールドを処理するためのユーティリティとして、スクリプトのみ存在しています。

FieldMgr (フィールド管理) シーンについて

タイルを管理するなら TileMgr (タイル管理) では…？　と思ったかもしれませんが、FieldMgr はタイル以外にも「選択カーソル（ユーザーからの入力）」を管理していることもあり、この名前としました。

もし TileMgr が存在しないことに疑問を感じる場合には、入力処理を切り離して別々のモジュールとしても良いのかもしれません。

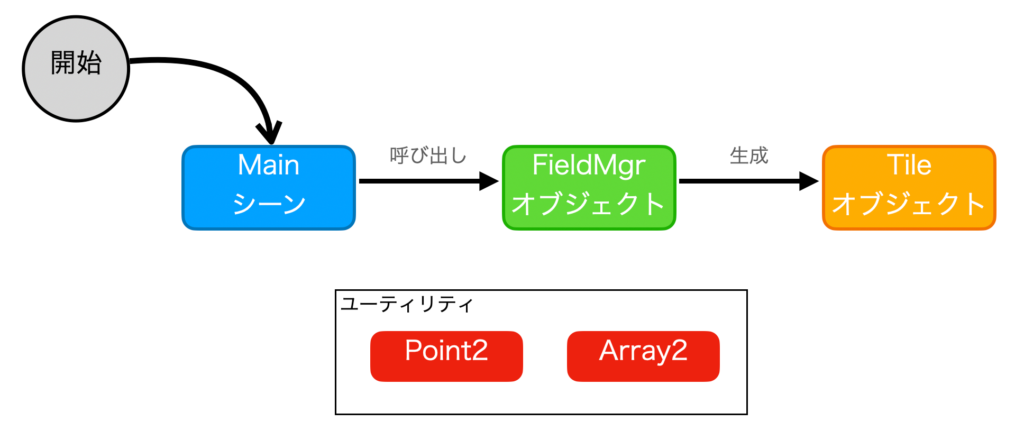
ユーティリティクラスについて

Point2とは

Point2とは整数値 (int) で x と y の値を持つクラス (ベクトル) です。Godot Engine には Vector2 というベクトルクラスがありますが、こちらは浮動小数値 (float) だったので別途定義しています。

なお、Godot 4.x 以降では Vector2i という整数値のベクトルが用意されているので、Godot 4.x 以降であればそちらを使ってみても良いかもしれません。

GODOT DOCS > Vector2i

Array2とは

Array2とは2次元配列を扱いやすいように拡張したクラスです。次に説明するグリッド座標系を扱うのに便利なクラスとなっています。

座標系の扱い

マッチ3ゲームのような グリッド(格子状) に配置したオブジェクトを扱うゲームを作る場合には、「座標系の扱い」について理解しておく必要があるので説明します。

今回作るマッチ3ゲームでは、以下の3つの座標系を使用します。

1. ワールド座標系: 実際に画面にオブジェクトを表示する座標系。今回はスクリーン座標系と同義
2. グリッド座標系: グリッドを基準とした2次元の座標系
3. インデックス座標系: グリッド座標系を「1次元」に変換した座標系

ワールド座標系以外は一般的でない用語なので、今回作るゲームの専用の用語として理解してもらえればと思います。

ワールド座標系とは

ワールド座標系とは、ゲーム画面に表示されている実際の座標です。今回のゲームは画面がスクロールしないので「スクリーン座標系」と同じもの考えて問題ありません。

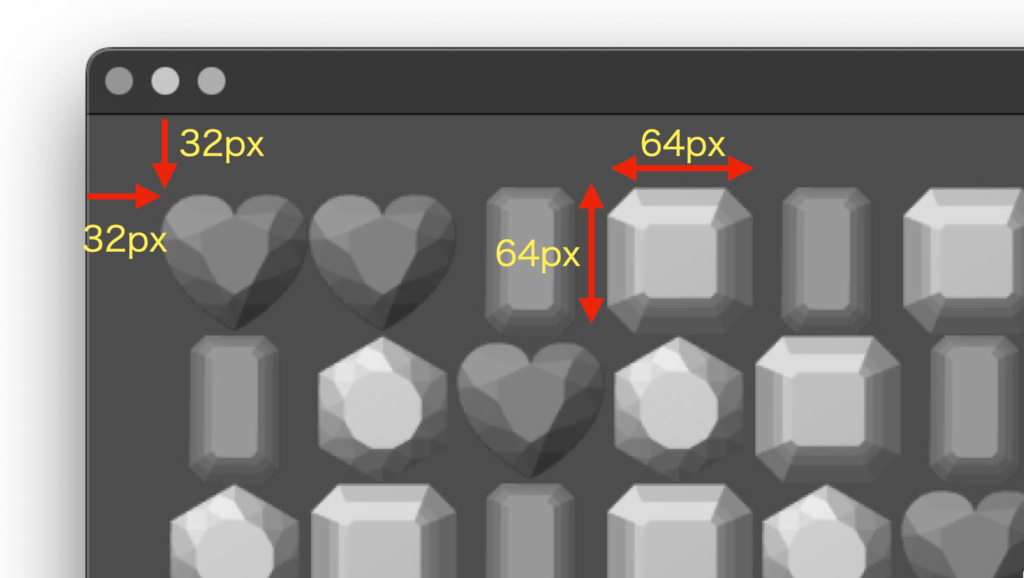
今回のゲームでは、タイルの描画開始座標が (x, y) = (32, 32) となっていて、1つのタイルサイズが 64×64 です。

そのため、例えば黄色で囲んだタイルの座標は以下の計算で求められ、ワールド座標は (x, y) = (288, 96) の位置に存在します。

ワールド座標の描画開始位置の定数

FiledMgr.gd の定数は以下のように定義されています。

# ----------------------------------------
# 定数.
# ----------------------------------------
const OFS_X = 64 # フィールドの描画オフセット(X).
const OFS_Y = 64 # フィールドの描画オフセット(Y).

ここで描画オフセットの値が “32” ではなく “64” となっているのは、タイルの描画基準が中央となっているためとなります。(64-32=32 が最終的な値となるためです)

グリッド座標系とは

グリッド座標系とは、タイルをグリッド基準で考えたときの座標系です。

以下の白い四角の部分は、X方向では “4”、Y方向では “1” の場所にあるので、グリッド座標系では (gx, gy) = (4, 1) の位置に存在するといえます。

グリッド座標系を使用する理由

なぜグリッド座標系を使用するのかというと、タイルの消去判定が楽に行えるためです。

ワールド座標系だと、例えば隣にあるタイルを調べるためにタイルのサイズぶん位置を移動する必要があります (今回であれば 64px)。

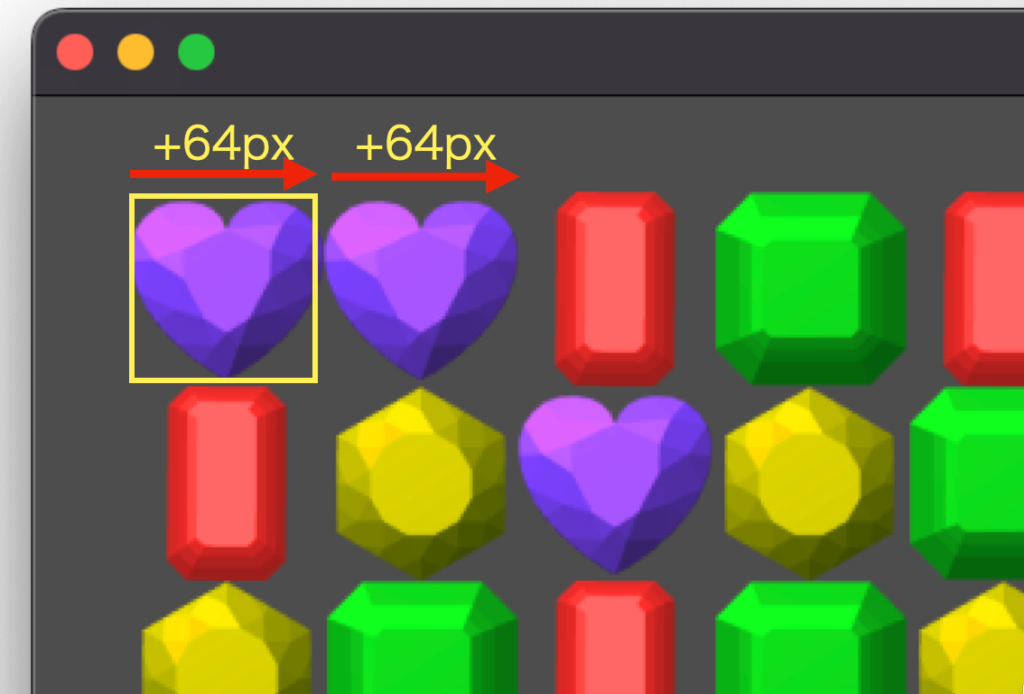
それに対してグリッド座標系では、1つ移動するだけで隣のタイルを調べることができます。

といったように「プログラム上での情報の扱いやすさ」がグリッド座標系を採用する理由です。

そしてグリッド座標系を使用することで得られる、もう一つのメリットが「すべてのタイル情報を2次元配列で扱うことができる」ことです。

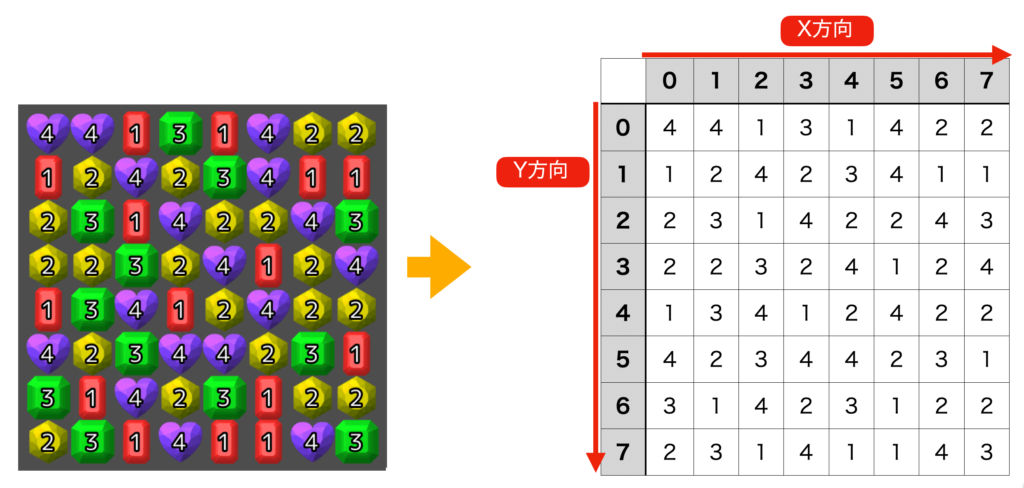
タイルの種類にIDを割り振ると、2次元の数値の配列でフィールド情報を表現でき、消去判定がやりやすくなります。

インデックス座標とは

インデックス座標系とは、グリッド座標系を1つの単位だけ(通し番号)で管理できるようにしたものです。

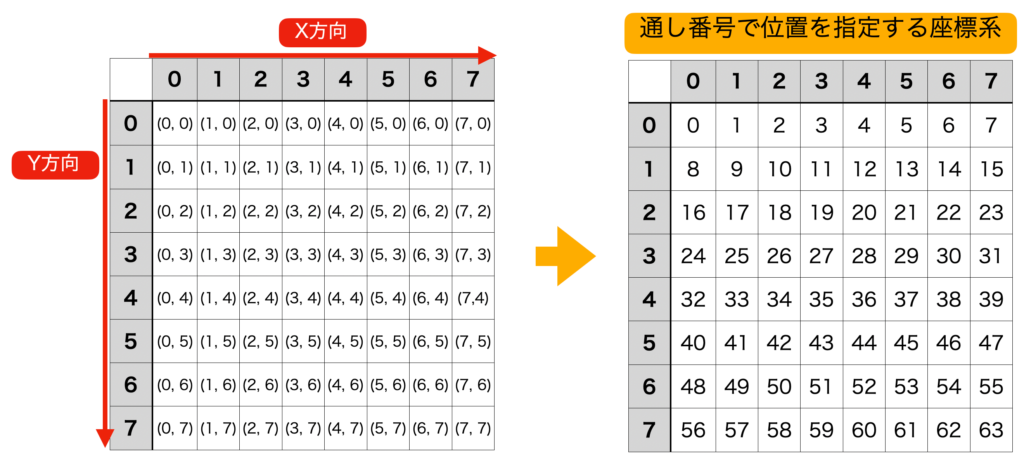
例えば、グリッド座標系で (x, y) = (4, 1) の位置は、インデックス座標系では「12」となります。

インデックス座標系は必須か？

インデックス座標系を使う利点は、1つの整数値で位置を表現可能であることです。

グリッド座標系は XとY の値を必要とするためクラスの定義が必要となりますが、インデックス座標系は int型で表現できるという扱いやすさがあり採用しています。

また int はプログラム言語が用意する基本的なデータ型(プリミティブ型)でありプログラムの実行効率が良いという理由もあります。

ただ、今回のようなゲームであれば実行速度も問題にはならないので、無理に使用する必要はないのかもしれません。

「見た目」と「処理」の分離

プログラムを上達するための基本的な考えとして「見た目」と「処理」を分離する、ということが良く話題に上がります。

今回の例であれば「ワールド座標系」は見た目で、「グリッド座標系」は処理となります。ゲームプログラムをするときには、このように見た目の表示に必要な値と、内部処理で使用する値を明確に分離しておくことで、効率よくプログラムを実装するケースが数多く存在することは知っておくと良いと思います。

以下、「見た目」と「処理」を分離している例です。

ガチャの演出：ガチャを引くボタンを押したタイミングで何ができるか確定している。そのため演出をスキップしてもしなくても結果は同じとなる
ターン制RPG：全員のコマンド入力が確定したタイミングでバトル結果をすべて計算する。それによりバトルの高速化処理が柔軟に行える
スーパーロボット大戦の演出：攻撃が当たるかどうかは攻撃を決定したときに確定している

座標系の相互変換

今回のゲームでは3つの座標系を扱いますが、座標系はお互いに変換可能です。

変換	計算方法
ワールド(w)→グリッド(g)	gx = (wx – オフセット(X) ) / タイルサイズ gy = (wy – オフセット(Y) ) / タイルサイズ
グリッド(g)→インデックス(idx)	idx = (gy * タイルの横の数) + gx
インデックス(idx)→グリッド(g)	gx = idx % タイルの横の数 gy = idx / タイルの横の数
グリッド(g)→ワールド(w)	wx = (gx * タイルサイズ) + オフセット(X) wy = (gy * タイルサイズ) + オフセット(Y)

※除算(割り算)のとき、端数はすべて切り捨てます。

相互に変換可能である性質を使って、画面に最終的に表示する場合は「ワールド座標系」を使用していますが、消去判定には「グリッド座標系」「インデックス座標系」に変換して判定を行う、という実装をしています。

それぞれの変換関数の定義

これらの座標変換は以下のスクリプトで行っています。

■ワールド座標系をグリッド座標系へ変換

# ワールド座標をグリッド座標系に変換する.
func world_to_grid(world:Vector2) -> Point2:
	var p = Point2.new()
	var half = TILE_SIZE / 2.0 # 中央揃えなので.
	var i = int((world.x - OFS_X + half) / TILE_SIZE)
	var j = int((world.y - OFS_Y + half) / TILE_SIZE)
	if i < 0 or WIDTH <= i:
		i = -1
	if j < 0 or HEIGHT <= j:
		j = -1
	if i == -1 or j == -1:
		# 無効な値なのでリセット.
		p.reset()
		return p
	
	p.set_xy(i, j)
	return p

■グリッド座標系からインデックス座標系への変換

# インデックス(1次元)に変換する.
func to_idx(i:int, j:int) -> int:
	return j * width + i

■インデックス座標系からグリッド座標系への変換

# インデックスを(x, y)に変換する.
func to_x(idx:int) -> int:
	return idx % width
func to_y(idx:int) -> int:
	return idx / width
func idx_to_pos(idx:int) -> Point2:
	var x = to_x(idx)
	var y = to_y(idx)
	return Point2.new(x, y)

■グリッド座標系からワールド座標系への変換

# グリッド座標系をワールド座標系に変換する.
func to_world(x:float, y:float) -> Vector2:
	# タイル座標系をワールド座標に変換する.
	var px = OFS_X + TILE_SIZE * x
	var py = OFS_Y + TILE_SIZE * y
	return Vector2(px, py)

消去判定

繰り返しの説明となってしましますが、消去判定は2次元の配列 (グリッド座標系) で行います。

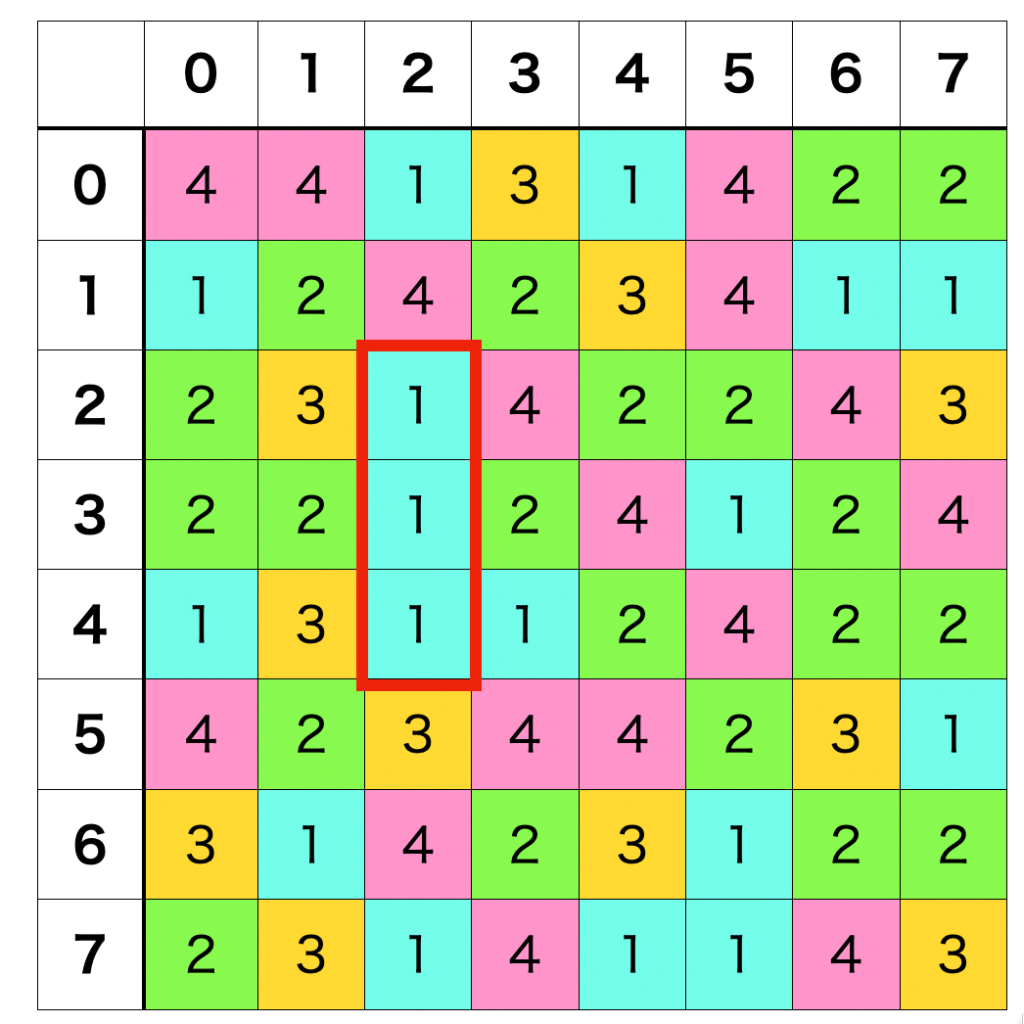
マッチ3パズルは「上下または左右に3つ以上連続して同じタイルがある」とタイルを消去できるルールとなっています。そのため上記画像の例であれば、

(x, y) = (2, 2)
(x, y) = (2, 3)
(x, y) = (2, 4)

この３つのタイルが消去可能です。

消去タイルを探索する方法は以下の通りとなります。

1. 左上のタイルから順番に探索開始ポイントを決める
2. 探索開始ポイントの上下または左右方向に同じタイルがあるかどうかを調べる
3. 同じタイルが3つ以上連続していれば消去対象となる
4. 最後のタイルになるまで1〜3の探索を繰り返す

このあたりは経路探索プログラミングに慣れていれば難なくできると思いますが、そのあたりが不慣れな人のために簡単に説明します。

1. 左上のタイルから順番に経路探索ポイントを決める

まずは探索を開始するポイントを決めます。左上から順番に開始タイルから基準に消去可能なタイルかどうかを調べていきます。

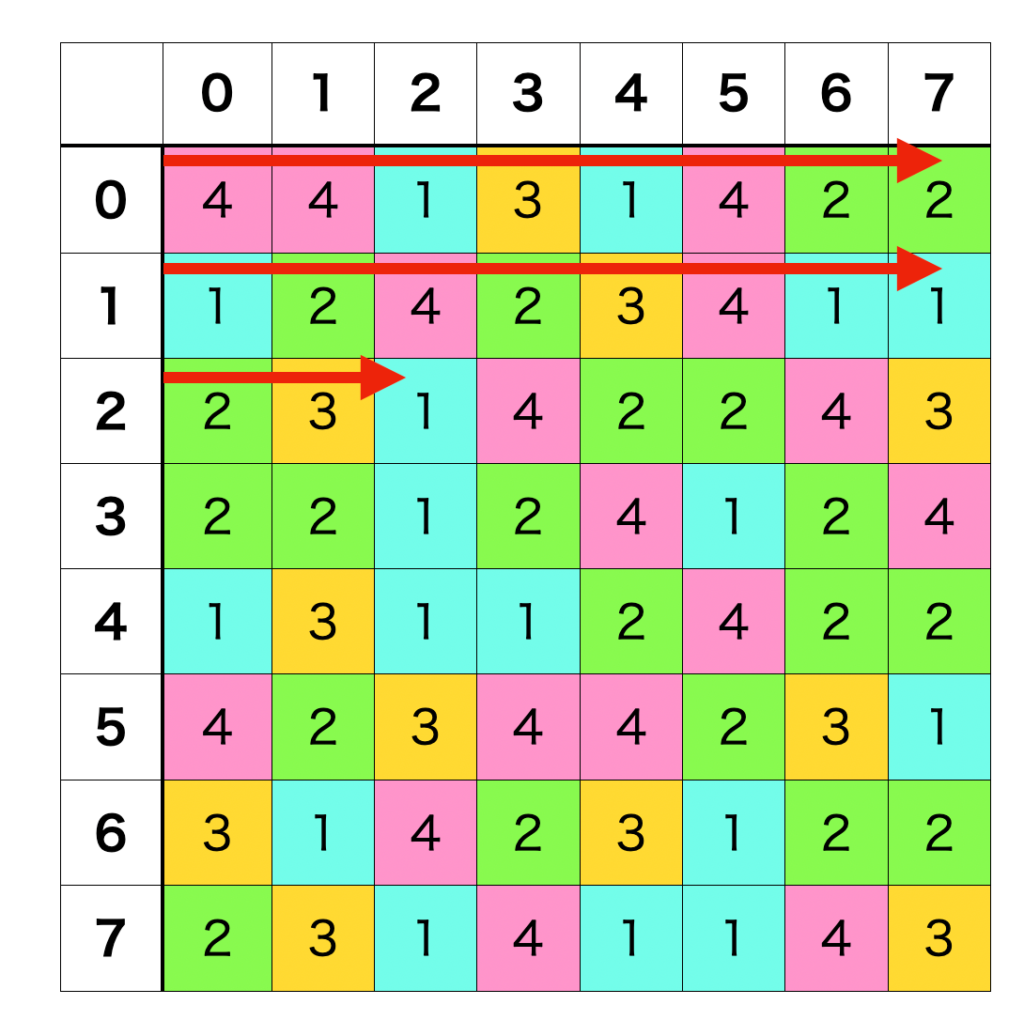
スクリプトでは FieldMgr.gd の check_erase() が消去チェックの関数で、2重のfor文のループで開始タイルを決めています。

# 消去チェックする.
# @return 消去するインデックスのリスト.
func check_erase() -> PoolIntArray:
	var erase_list = PoolIntArray()
	
	# 消去判定用の2次元配列.
	var tmp = Array2.new(WIDTH, HEIGHT)
	
	for j in range(_field.height):
		for i in range(_field.width):
			# 開始タイルを決める.
			var n = _field.getv(i, j)
			if n == Array2.EMPTY:
				continue	 # 空なので判定不要.
			
			# 上下と左右を分けて判定する.
			...

2. 探索開始ポイントの上下または左右方向に同じタイルがあるかどうかを調べる

次に開始タイルから上下または左右方向を調べて、連続して同じ番号のタイルであるかどうかをチェックします。

例えば (x, y) = (0, 0) が消去可能かどうかを調べるには、”4″ のタイルが3つ以上連続しているかどうかを調べます。

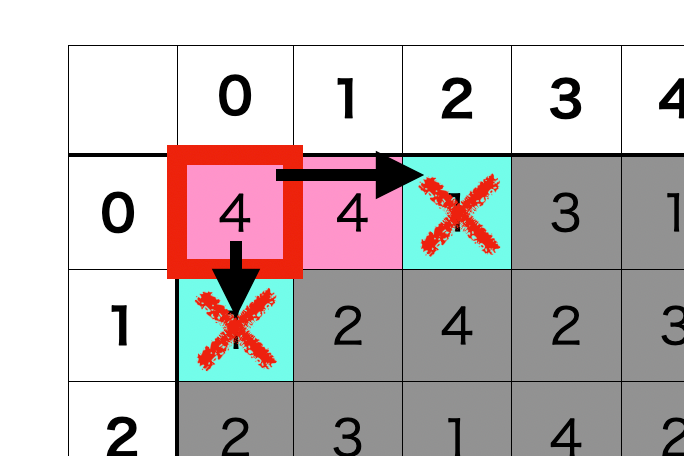
下方向を調べた場合、(x, y) = (0, 1) は “1” のタイルなので、縦方向には同じタイルはないこととなります。そして、右方向には隣に “4” がありますが、その隣が “1” なので探索は終了となります。

このあたりの処理を行っているのが FieldMgr._check_erase_recursive() ですが、よく見るとこの関数内で自身 _check_erase_recursive() を呼び出しています。

# 消去チェック (再帰処理用).
func _check_erase_recursive(tmp:Array2, n:int, cnt:int, x:int, y:int, vx:int, vy:int) -> int:
	# 移動先を調べる.
	var x2 = x + vx
	var y2 = y + vy
	if tmp.getv(x2, y2) == eEraseType.NOT:
		# 探索済み.
		return cnt
	
	var n2 = _field.getv(x2, y2)
	if n != n2:
		# 不一致なので消せない.
		tmp.setv(x2, y2, eEraseType.NOT)
		return cnt
	
	# 消せるかもしれない.
	cnt += 1
	tmp.setv(x2, y2, eEraseType.REMOVE)
	
	# 次を調べる.
	return _check_erase_recursive(tmp, n, cnt, x2, y2, vx, vy)

これは関数の再帰呼び出しで、呼び出し先でも同じ処理を繰り返し行いたい場合に、この書き方は便利です。

経路探索では同じ処理を繰り返して探索範囲を広げていく…、という処理がよく使われます。再帰呼び出しで注意しなければいけないのが、すでに探索した経路を再度呼び出して「無限ループ」が発生する問題ですが、今回のサンプルではtmpという2次元配列の変数に探索結果を保持することで無限ループになるのを防いでいます。tmp変数については後の項で説明をします。

3. 同じタイルが3つ以上連続していれば消去対象となる

探索が終了したら、連続しているタイルが3つ以上であるかどうかをチェックします。

(x, y) = (0, 0) のタイルは2つだけなので消せない…、ということとなります。

そのあたりの処理を行っているのがFieldMgr.check_erase() の以下のコードですね。

				# 上下を調べる.
				var tbl = [[0, -1], [0, 1]]
				if k == 1:
					# 左右を調べる.
					tbl = [[-1, 0], [1, 0]]
				
				#  消去判定の再帰処理呼び出し.
				for v in tbl:
					cnt = _check_erase_recursive(tmp, n, cnt, i, j, v[0], v[1])
				
				if cnt >= ERASE_CNT:
					# ERASE_CNT以上連続していれば消せる.
					var list = tmp.search(eEraseType.REMOVE)
					erase_list.append_array(list)

“ERASE_CNT” は “3” なので、3つ以上連続していれば消去対象として消去リスト (erase_list) に追加しています。

探索処理の高速化するための2次元配列について

check_erase() 内で定義されている、tmpという Array2 の変数について補足します。

	# 消去判定用の2次元配列.
	var tmp = Array2.new(WIDTH, HEIGHT)

この変数は、探索を高速化するためのキャッシュ用として使っています。例えば経路探索を行う場合、すでに探索済みの場所をスキップすることで高速化を行うケースがありますが、 tmp変数はそういった高速化を行うために用意されたものとなります。

以下、tmp変数に格納する値 (探索状態) です。

# 消去種別 (消去判定で使用する).
enum eEraseType {
	EMPTY  = 0 # 空.
	NOT    = 1 # 検索済み(消さない).
	REMOVE = 2 # 消去対象.
}

これを使用したときの流れを説明します。

まず探索を開始する前は経路探索高速化 Array2 の値はすべて「0 (EMPTY)」にします。

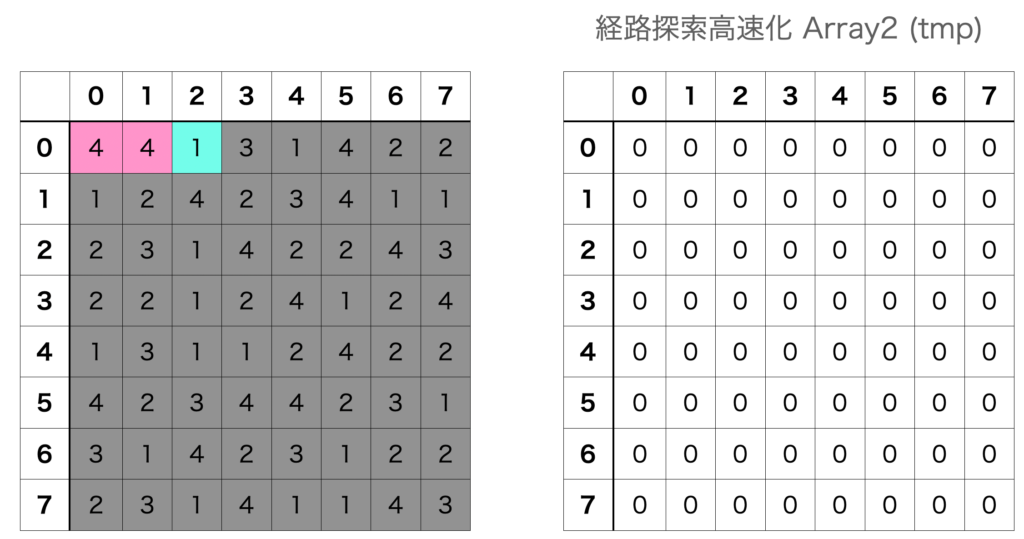
次に探索開始ポイントが決まった場合は “2 (REMOVE)” を設定します。

そして探索結果を設定することで、重複した場所を探索してしまう無駄をなくすことができます。

そして最終的には「2 (REMOVE)」の場所が3つ以上あるかどうか、という判定となります。

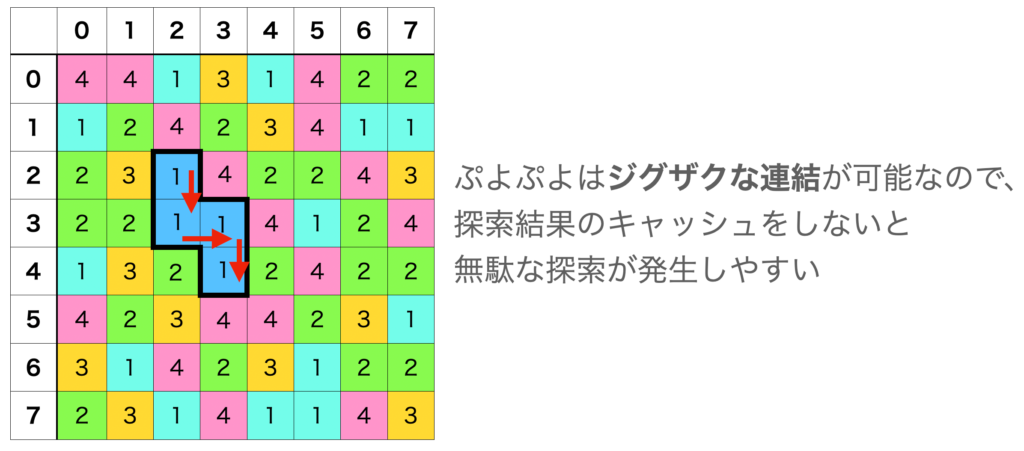
と長々と説明したものの、実は今回のマッチ3ゲームは直線方向のみに連結するため、高速化にはあまり貢献できていません（消去判定の結果を保持する用途）。

これが「ぷよぷよ」のように隣接するのであれば直線でなくてもよい消去ルールの場合、このキャッシュの恩恵が得られるようになります。

タイルの落下と着地判定

タイルの落下処理について

タイルの落下はグリッドの境界をまたぐ値で移動します。

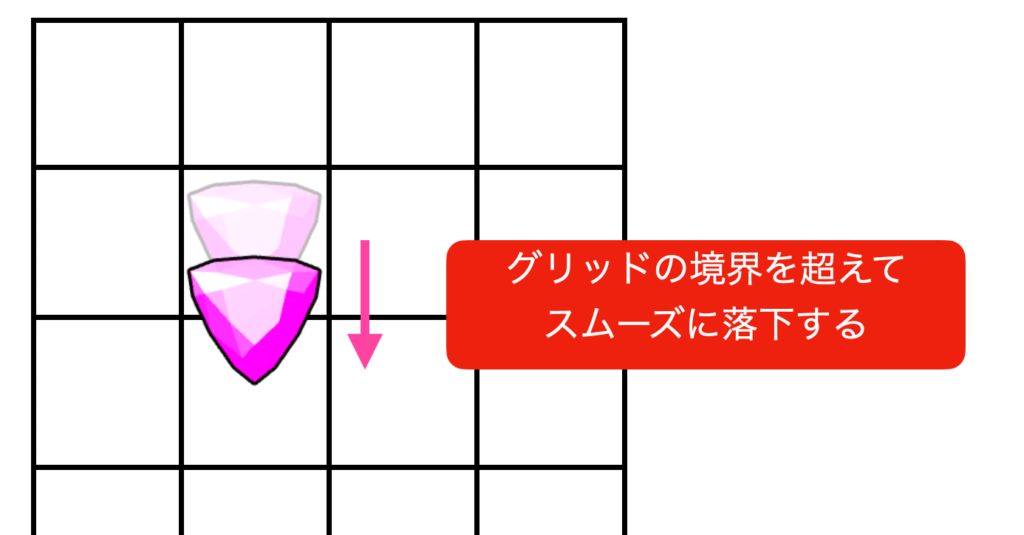
そのため整数値のグリッド座標系では判定できないので、int(整数値) ではなく float(浮動小数値) を使用して落下と設置判定をするようにしました。

# 現在のグリッド座標.
var _grid_x:float = 0
var _grid_y:float = 0

そして重力（落下）の処理は Tile.proc() で行っています。

	match _state:
		eState.HIDE: # 非表示.
			visible = false
		eState.FALLING: # 落下中.
			_label.text = "F"
			# 重力を加算.
			_velocity_y += GRAVITY_Y	 * delta
			# 速度を位置に加算.
			_grid_y += _velocity_y
			if _check_fall() == false:
				# 移動完了.
				fit_grid()
				_velocity_y = 0
				_state = eState.STANDBY

タイルは “_state” という状態変数を持ち、状態が eState.FALLING (落下中) の場合のみ重力による移動を行っています。

本来グリッド座標系は整数値なので、この方法はややイレギュラーですが、落下中にはタイルの相互作用（消去やプレイヤーによる操作）が発生しないという特性があるため、今回のゲーム仕様では問題ないかなと思っています。

なぜ独自の更新関数を実装したり、衝突や重力処理を自作しているのか？

Godot Engineには、標準の更新関数 (_process) や衝突判定、物理エンジンによる重力処理が実装されていますが、今回のサンプルでは使用していません。

理由としては、処理の順序が重要となるパズルゲームでは、ゲームエンジン固有の機能を使うよりも、自作したほうが「更新タイミング」や「チェック処理」を仕様に合わせて細かく制御できるためです。

パズルゲーム以外にも、処理順序が重要となるターン制ゲームや、UIの入力タイミングを細かく制御をしたい場合などでも自作した方が有効な場合があります。

落下の着地判定

タイルの着地判定は Tile._check_fall() で行っています。

# 落下チェック.
func _check_fall() -> bool:
	if FieldMgr.check_hit_bottom(self):
		return false
	return true

正確には以下の順で関数が呼び出されるので、

1. Tile._check_fall(): 落下が必要かどうか (trueなら落下処理を開始。falseなら落下処理を終了)
2. FieldMgr.check_hit_bottom(tile:TileObj): 指定したタイルの下にタイルがあるかどうか
3. Tile.check_hit_bottom(tile:TileObj): 指定のタイルが足元で接触しているかどうか

最終的に呼び出される Tile.check_hit_bottom() が下にあるタイルとの衝突判定を行っています。

# 下のタイルと衝突しているかどうか
# @param tile 判定する下のタイル 
func check_hit_bottom(tile:TileObj) -> bool:

	# 衝突チェックするタイルの情報を取り出す.	
	var obj_id = tile.get_instance_id() # インスタンス番号
	#var number = tile.get_id() # タイル番号 (デバッグ用)
	var tile_x = tile.get_grid_x() # グリッド座標(X)
	var tile_y = tile.get_grid_y() # グリッド座標(Y)
	
	# ユニークIDを比較.
	if get_instance_id() == obj_id:
		return false # 自分自身は除外.
	
	if _grid_x != tile_x:
		return false # 別のX座標のブロック
	
	if _grid_y > tile_y:
		return false # 対象のタイルがそもそも上にあるので判定不要.
		
	var bottom = _grid_y + 0.5 # 上のブロックの底
	var upper = tile_y - 0.5 # 下のブロックのトップ
	if bottom < upper:
		return false # 重なっていない.
	
	# 更新タイミングの関係でめり込んでいたら押し返す.
	_grid_y -= (bottom - upper)
	
	return true

この関数では以下の「4つの判定」と「1つの処理」を行っています。

1. 自分自身とは衝突判定を行わない
2. X座標が異なる場合は衝突しない
3. 自身よりも上の位置にあるタイルは衝突しない
4. 自身の底(bottom) が対象のトップ(upper) よりも下にあれば衝突したとみなす
5. 衝突していた場合は、対象のタイルとの重なりを解消（押し戻しする）処理を行う

1. 自分自身とは衝突判定を行わない

Tile.check_hit_bottom() は、自分自身を含むタイルとの判定を行います。そのため自分自身とも判定をおこなってしまうので、それを除外する判定となります。

Godot Engine では get_instance_id() でユニークな(他と重複しない)インスタンスIDを取得できるので、それが一致するかどうかで判定できます。

2. X座標が異なる場合は衝突しない

タイルが移動するのは Y方向だけなので、X座標が異なる場合は衝突しないので除外します。

3. 自身よりも上の位置にあるタイルは衝突しない

厳密にはタイルの上半分の部分で衝突する可能性がありますが、着地するかどうかを判定したいだけなので、自身の位置よりも上にあるタイルは判定を除外します。

4. 自身の底(bottom) が対象のトップ(upper) よりも下にあれば衝突したとみなす

下のタイルと衝突判定するだけで良いので、自身の底(bottom)の位置を計算し、対象のトップ(upper)を超えていないかを判定します。

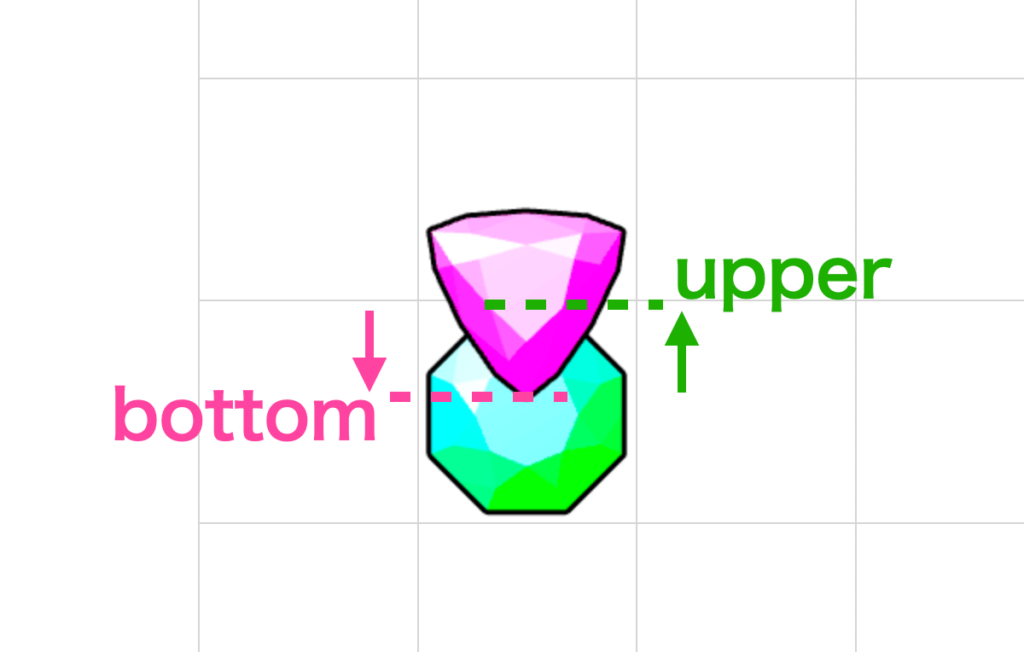
上記の図のようにめり込みが発生してれば、衝突したとみなします。

	var bottom = _grid_y + 0.5 # 上のブロックの底
	var upper = tile_y - 0.5 # 下のブロックのトップ
	if bottom < upper:
		return false # 重なっていない.

そして次の「押し戻し処理」を行います。

5. 衝突していた場合は、対象のタイルとの重なりを解消（押し戻しする）処理を行う

衝突が発生していたらそのめり込みを解消するためにタイルを押し戻します。

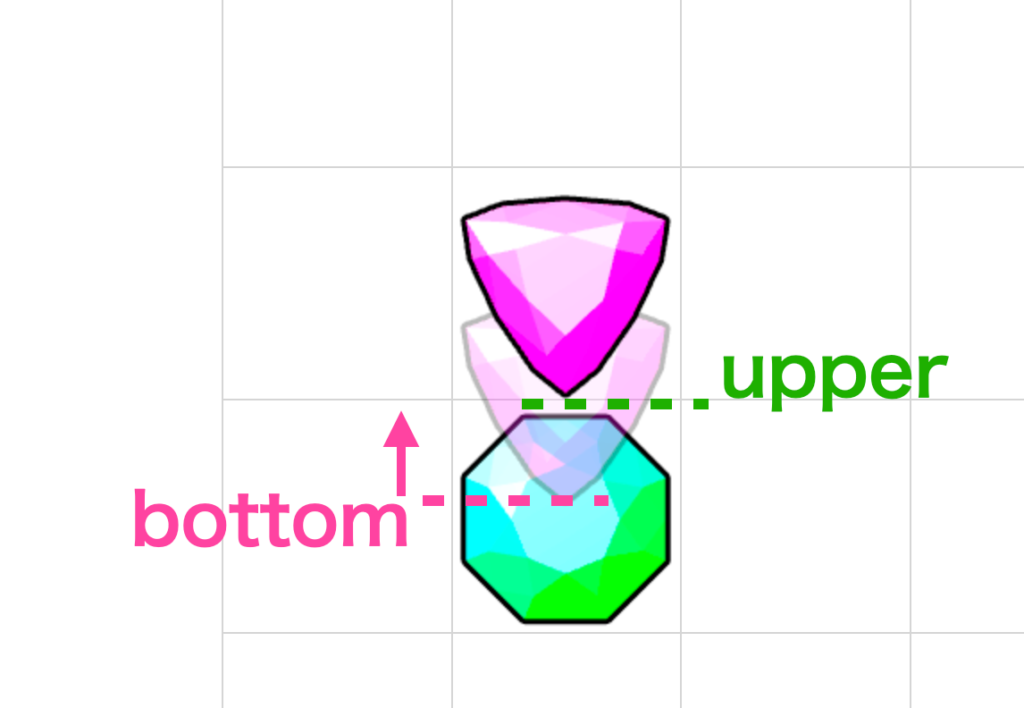
	# 更新タイミングの関係でめり込んでいたら押し返す.
	_grid_y -= (bottom - upper)

今回のサンプルを拡張するヒント

今回のサンプルは落ちものパズルの基本的な要素のみなので、もっとゲームらしくするには以下の機能を実装する必要があります。

制限時間を入れて、時間がなくなるとゲームオーバー
お邪魔ブロック（簡単には消せないタイル）を出現させる
タイルをどう動かしても消去ができなくなった判定を入れて、その状態をゲームオーバーにしたりリセットするなどの対応を入れる

最後の要素は実装が間に合わなかったので入れていないですが、おそらく入れ替えするパターンを総当りで判定して消去可能なポイントを探す…というアルゴリズムになりそうです。

マッチ3ゲームとしての純粋な面白さを追求する場合

純粋なマッチ3ゲームとしてゲーム性を拡張したい場合には、本家の Bejeweled シリーズを分析するのがおすすめです。PCであれば Steam版の Bejeweled® 3 がありますし、iOS や Android にはBejeweled Classic (iOS版 / Android版) というアプリで移植されています。

タイルを4つ以上つなげるとまとめて消すことのできるタイルに変化したり、 ポーカーのルールを採用しているゲームモードがあったりと、マッチ3ゲームの純粋な面白さを追求した要素やゲームモードがあってとても勉強になります。

Bejeweled のゲームシステムやモードは以下のページにまとめています。

Bejeweled

RPG要素を足す場合

もう1つのアプローチとしてRPG要素（HPや敵を出現させる）を足す方法もあります。

たくさんタイルを消すほど敵にダメージを与えることができる
一定時間経過で敵が攻撃してプレイヤーにダメージを与えたりお邪魔ブロックを出現させる

もしRPG要素を足す場合には「PuzzleQuest: Challenge of the Warlords」「Shovel Knight Pocket Dungeon」あたりが参考になるかもしれません。

PuzzleQuest: Challenge of the Warlords
(出典:D3 Go!)

Shovel Knight Pocket Dungeon
(出典:Yacht Club Games)

PuzzleQuest: Challenge of the Warlords について

PuzzleQuest: Challenge of the Warlords (パズルクエスト〜アガリアの騎士〜) では、オセロや将棋のようにプレイヤーと敵が交互にタイルを動かします。また、4つ以上まとめてタイルを消すと「ターンを継続」することができます。

タイルは以下の種類のものが存在します。

マナ：スキルを使用するために必要なマナを獲得する
ドクロ：相手にダメージを与える
お金：お金が増える
経験値：経験値が増える