この記事では、矩形状に区切られたマップとの衝突・応答判定を行う方法の解説します。

例えば、こういったRPGツクールでよく見られるマス目で区切られたマップです。このときのプレイヤーと、赤くしている障害物との当たり判定の実装方法について紹介します。
目次
矩形マップは、縦軸・横軸からなる2次元の表です。
なので、たいてい矩形マップを読み込むと、2次元の配列になり、以下のように「座標」をキーに、マップデータを取得することになります。
/**
* 座標を指定してマップデータを取得する
* @param x, y 座標
* @return マップデータ
*/
int getMapData(int x, int y) {
return map_data[x][y];
}衝突検知は矩形同士の当たり判定をやったことがある人なら簡単です。
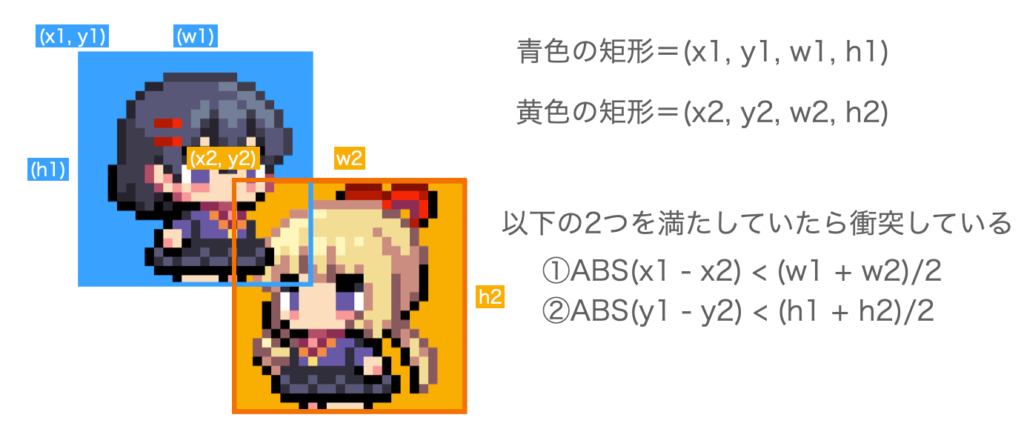
問題は衝突応答の判定になります。
衝突応答の処理
「衝突検知」は、移動後の座標が通過できない地形であった場合に 「衝突した!」という判定を返すだけです。それに対して「衝突応答」では「通過できる地形まで戻してやる」という処理をします。
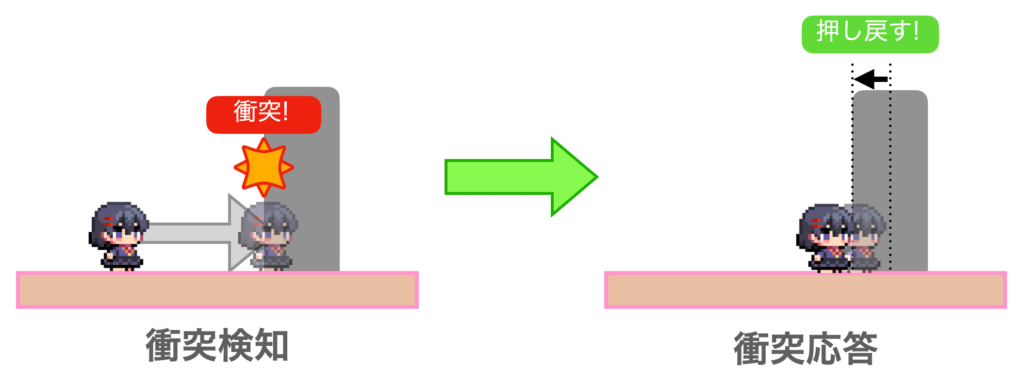
衝突応答を実装するには、縦軸横軸を分けて考えるとシンプルに実装できます。 というのは、斜め移動できるゲームの場合、縦軸の移動量と横軸の移動量を同時に処理しようとすると、 どちらの戻してやるのが良いのかがわからなくなるからです。
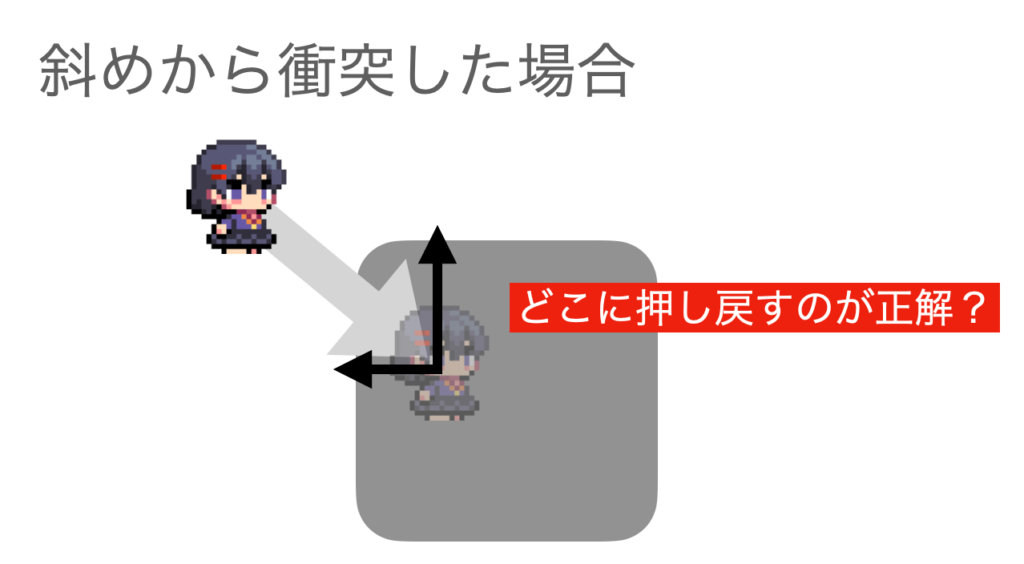
これを解決するには、XYの移動を軸ごとに分離して判定します。

- X方向に3移動してみる
- 移動後の座標と地形との衝突判定
- 衝突していた場合、移動量が正であれば、衝突した地形の左に戻す。移動量が負であれば、衝突した地形の右に戻す
次にY軸の移動を行う
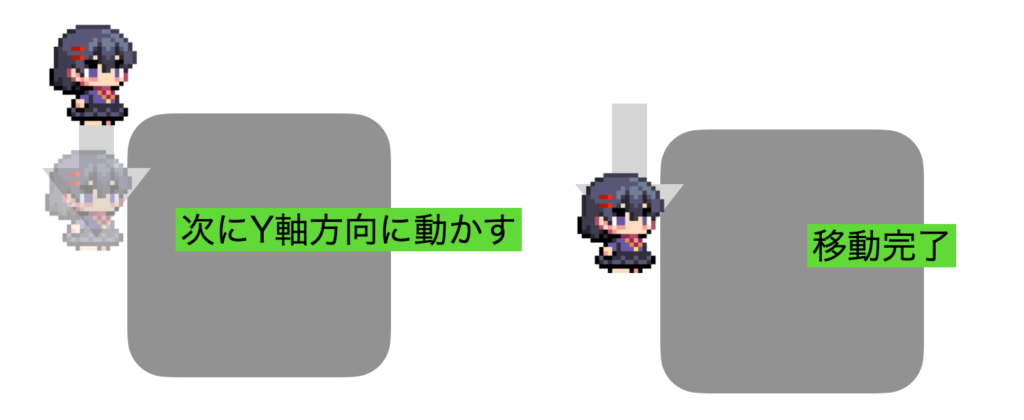
- Y方向に6移動してみる
- 移動後の座標と地形との衝突判定
- 衝突していた場合、移動量が正であれば、衝突した地形の上に戻す。移動量が負であれば、衝突した地形の下に戻す
というように、衝突応答の判定がシンプルに行えるようになります。
ここまでは単なる矩形との判定です。
説明が前後してしまっていますが、 矩形マップにおける座標は、チップがある座標であって スクリーン座標ではありません。
例えば、チップサイズが32×32である場合、 スクリーン上での(x,y)=(320,256)は、 矩形マップでは(x,y)=(320/32,256/32)=(10,8)となります。
ここで問題となるのは以下の状態です。
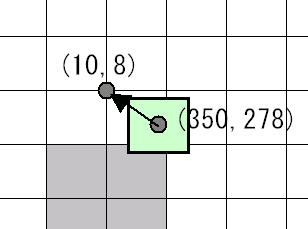
スクリーン上の(x,y)=(350,278)にプレイヤーがいるとします。 この場合のマップ座標は左上に引きずられ(x,y)=(350/32,278/32)=(10,8)になります。
灰色のところが通過できない地形とすると、 この場合、正常な当たり判定ができなくなり、めり込みが発生します。
この問題を回避するには、
- 移動前の座標を(px,py)
- 移動量を(dx,dy)
- 半径(サイズ)を(rx,ry)
- チップサイズを(chip)
とすると、
- X方向のみへ移動した座標を求める(px+dx, py)=Pとする
- 上側地形との当たり判定を考慮するP+(0, -ry)=P_upper
- マップ座標に変換するP_upper/chip=P_upper_div_chip
- P_upper_div_chipとマップとの衝突判定を行う。衝突していた場合、
- 移動量が正であれば、衝突した地形の左に戻す
- 移動量が負であれば、衝突した地形の右に戻す
- 下側地形との当たり判定を考慮するP+(0, ry)=P_bottom/chip=P_bottom_div_chip
- P_bottom_div_chipとマップとの衝突判定を行う。衝突していた場合、
- 移動量が正であれば、衝突した地形の左に戻す
- 移動量が負であれば、衝突した地形の右に戻す
- Y方向のみへ移動した座標を求める(px, py+dy)=Pとする
- 左側地形との当たり判定を考慮するP+(-rx, 0)=P_left
- マップ座標に変換するP_left/chip=P_left_div_chip
- P_left_div_chipとマップとの衝突判定を行う。衝突していた場合、
- 移動量が正であれば、衝突した地形の上に戻す
- 移動量が負であれば、衝突した地形の下に戻す
- 右側地形との当たり判定を考慮するP+(0, ry)=P_right/chip=P_right_div_chip
- P_right_div_chipとマップとの衝突判定を行う。衝突していた場合、
- 移動量が正であれば、衝突した地形の上に戻す
- 移動量が負であれば、衝突した地形の下に戻す
というように、場合分けを増やしてやることで、いい感じに衝突判定・応答をすることができます。
追記:めり込みを考慮しなくていい場合
ブロック崩しなど、衝突⇒反射という規則がある場合、
めり込みを考慮する必要はなく、移動量を反転させるだけでよいみたいです。
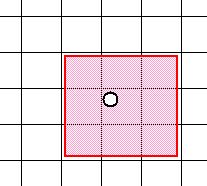
自分を中心に3×3の座標を調べて、衝突していたら移動量を反転する。
「ぐらびてぃっく ぶれいくあうと(OMEGAさん)」から抜粋
repeat BALL_MAX
if(ball_type(cnt) == BALL_TYPE_NULL) : continue
up_cnt = cnt
// 3×3のマップ座標を調べる
cx = -1 , 0 , 1 , -1 , 0 , 1 , -1 , 0 , 1
cy = -1 , -1 , -1 , 0 , 0 , 0 , 1 , 1 , 1
repeat 9
// ①ボール座標をマップ座標に変換
px = int(ball_x(up_cnt) / BLOCK_WIDTH) + cx(cnt)
py = int(ball_y(up_cnt) / BLOCK_HEIGHT) + cy(cnt)
if(px < 0 | px >= BLOCK_WIDTH_CNT | py < 0 | py >= BLOCK_HEIGHT_CNT) : continue
if(block_type(px,py) == BLOCK_TYPE_NULL) : continue
// ②スクリーン座標に戻して判定
if(absf((double(px) + 0.5) * BLOCK_WIDTH - ball_x(up_cnt,0)) < (BLOCK_WIDTH + BALL_SIZE) / 2.0 & absf((double(py) + 0.5) * BLOCK_HEIGHT - ball_y(up_cnt,0)) < (BLOCK_HEIGHT + BALL_SIZE) / 2.0){
if(block_type(px,py) != BLOCK_TYPE_HARD){
repeat 32
addeffect double(px * BLOCK_WIDTH + rnd(BLOCK_WIDTH)), double(py * BLOCK_HEIGHT + rnd(BLOCK_HEIGHT)) , double(rnd(32) - 16) * 0.3 , double(rnd(32) - 16) * 0.3 , EFFECT_TYPE_PERTIC , block_type(px,py)
loop
block_type(px,py) = BLOCK_TYPE_NULL
}
// ③移動量を反転
if(absf((double(px) + 0.5) * BLOCK_WIDTH - ball_x(up_cnt,0)) < absf((double(py) + 0.5) * BLOCK_HEIGHT - ball_y(up_cnt,0))){
if((double(py) + 0.5) * BLOCK_HEIGHT < ball_y(up_cnt,0) & ball_vy(up_cnt) < 0.0) : ball_vy(up_cnt) *= -(BLOCK_REFLECT)
if((double(py) + 0.5) * BLOCK_HEIGHT > ball_y(up_cnt,0) & ball_vy(up_cnt) > 0.0) : ball_vy(up_cnt) *= -(BLOCK_REFLECT)
}else{
if((double(px) + 0.5) * BLOCK_WIDTH < ball_x(up_cnt,0) & ball_vx(up_cnt) < 0.0) : ball_vx(up_cnt) *= -(BLOCK_REFLECT)
if((double(px) + 0.5) * BLOCK_WIDTH > ball_x(up_cnt,0) & ball_vx(up_cnt) > 0.0) : ball_vx(up_cnt) *= -(BLOCK_REFLECT)
}
}
loop
loop①ボール座標をいったんマップ座標に変換して、 ②スクリーン座標で円の判定を行っている
というのがポイントです。
(①でボール座標をマップチップの左上に引っ張り、②で中心に補正しているので円の判定でよい)