グリッド制のゲームでよく使う座標系について

今回は Grid-based (グリッド制) のゲームを作るときによく使われる座標系とその変換方法について書きます。

グリッド制のゲームでよく使う座標系について

グリッド制のゲームとは

グリッド制は、パズルゲームやターン制ストラテジー、昔ながらのターン制ローグライクゲームなどでよく採用されます。

ターン制ストラテジーの Into the breach
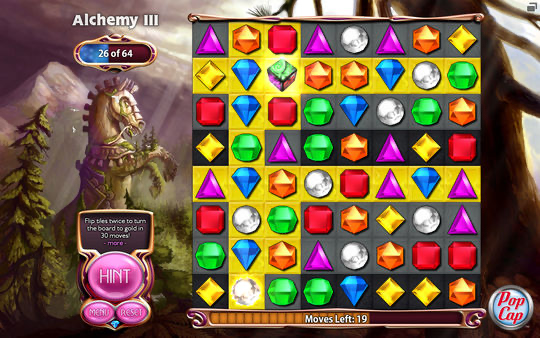
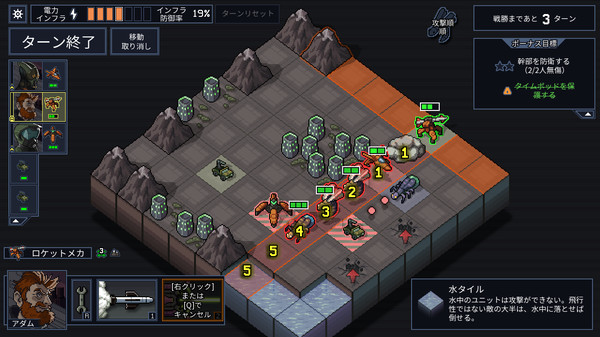
(出典:Subset Games)

ローグライクの風来のシレンplus5
(出典: Spike Chunsoft Co., Ltd.)

グリッドというマス目で区切られた単位でゲーム画面が構成されるので、思考が必要とされるパズルゲームやストラテジー要素があるゲームに向いています。

このような「マス目」を1つのデータの単位として扱うときに役立つ座標系とその変換方法について説明します。

グリッド制のゲームを作るときに便利な3つの座標系

グリッド制を採用したゲームでは、以下の3つの座標系を使用すると便利です。

1. ワールド座標系: 実際に画面にオブジェクトを表示する座標系。今回はスクリーン座標系と同義
2. グリッド座標系: グリッドを基準とした2次元の座標系
3. インデックス座標系: グリッド座標系を「1次元」に変換した座標系

なおグリッドの単位を「タイル」と呼ぶこともあります。これは Tile-matching game (タイルマッチングゲーム) で1つのパネルの単位をタイルとしている影響もあります。ところどころ「タイル」という名称を使っている部分もありますが、その場合はグリッドと読み替えてもらえればと思います。

1. ワールド座標系とは

ワールド座標系とは、ゲーム画面に表示されている実際の座標です。スクロールがないゲームであれば、スクリーン座標系と同じと考えて問題ありません。

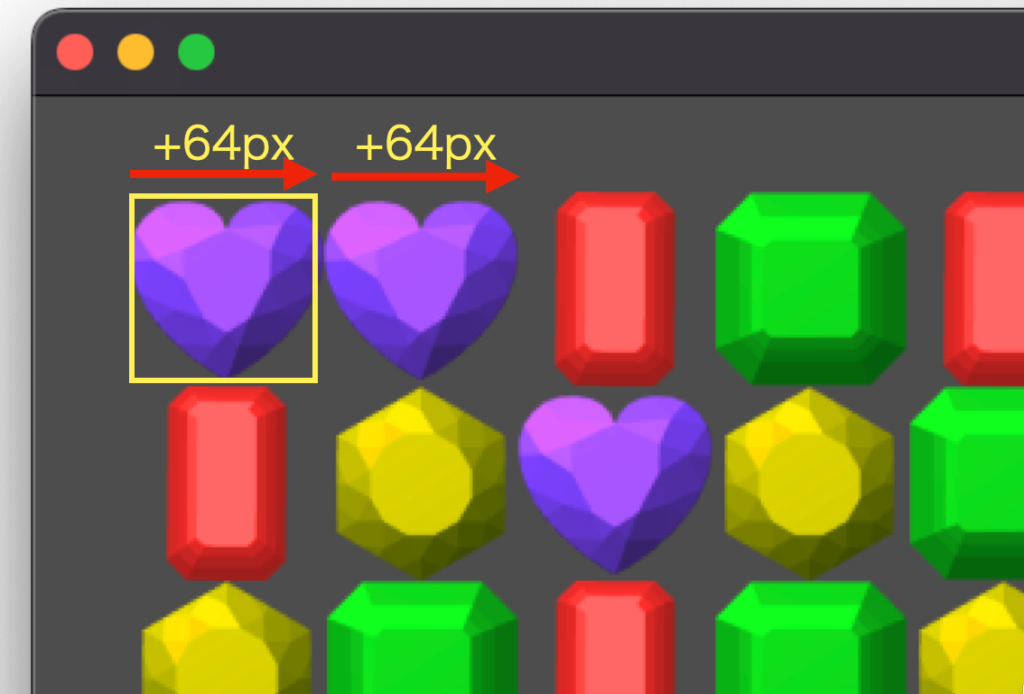
ワールド座標系は主に「左上の開始位置」「各グリッドのサイズ」の2つの要素で構成されます。

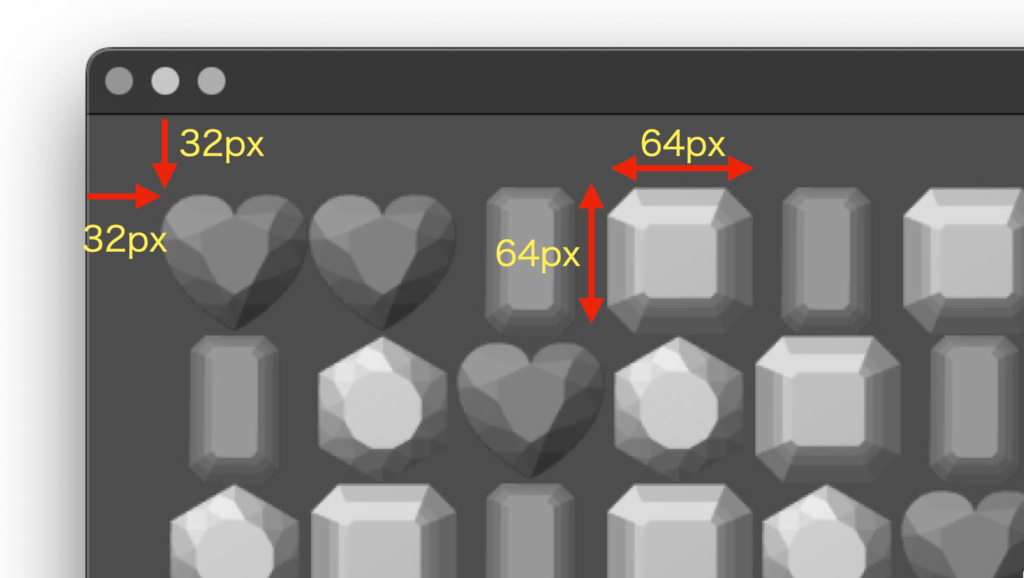
例えば、上記の画面構成の場合、タイルの描画開始座標が (x, y) = (32, 32) となっていて、1つのタイルサイズが 64×64 です。

そのため、例えば黄色で囲んだタイルの座標は以下の計算で求められ、ワールド座標は (x, y) = (288, 96) の位置に存在します。

2. グリッド座標系とは

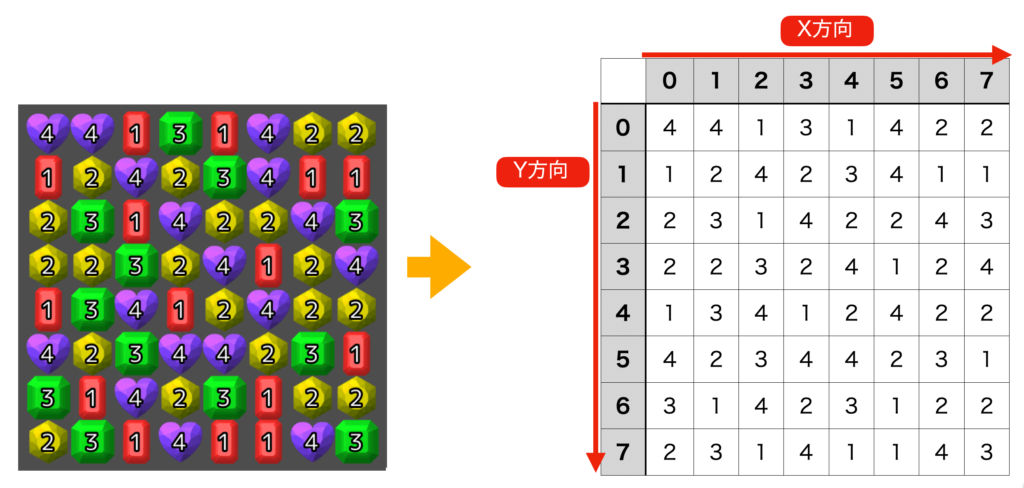
グリッド座標系とは、タイルをグリッド基準で考えたときの座標系です。

以下の白い四角の部分は、X方向では “4”、Y方向では “1” の場所にあるので、グリッド座標系では (gx, gy) = (4, 1) の位置に存在するといえます。

グリッド座標系を使用する理由

なぜグリッド座標系を使用するのかというと、タイルの消去判定が楽に行えるためです。

ワールド座標系だと、例えば隣にあるタイルを調べるためにタイルのサイズぶん位置を移動する必要があります (今回であれば 64px)。

それに対してグリッド座標系では、1つ移動するだけで隣のタイルを調べることができます。

といったように「プログラム上での情報の扱いやすさ」がグリッド座標系を採用する理由です。

そしてグリッド座標系を使用することで得られる、もう一つのメリットが「すべてのタイル情報を2次元配列で扱うことができる」ことです。

タイルの種類にIDを割り振ると、2次元の数値の配列でフィールド情報を表現でき、消去判定がやりやすくなります。

3. インデックス座標とは

インデックス座標系とは、グリッド座標系を1つの単位だけ(通し番号)で管理できるようにしたものです。

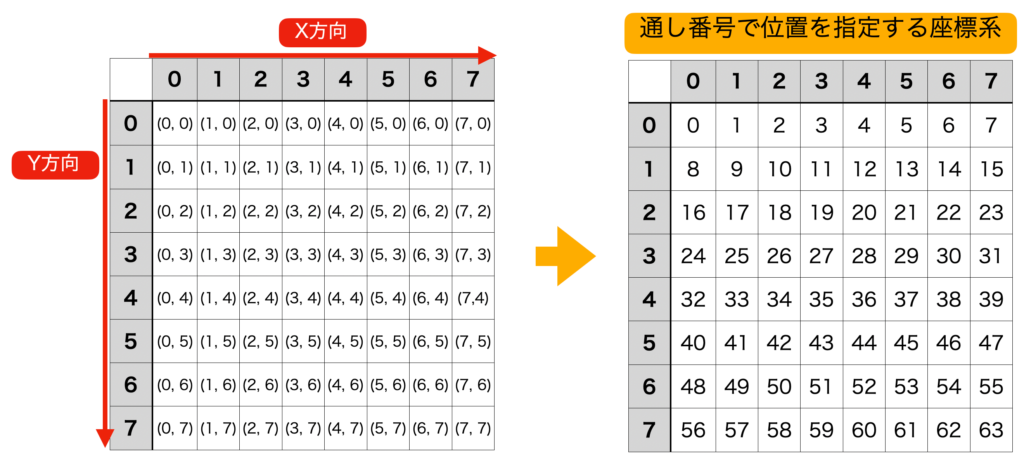
例えば、グリッド座標系で (x, y) = (4, 1) の位置は、インデックス座標系では「12」となります。

インデックス座標系は「1つの数値」で表現できるので、数値の1次元配列で管理できるのがメリットです。

それぞれの座標系の相互変換

それぞれの座標系は相互に変換が可能です。

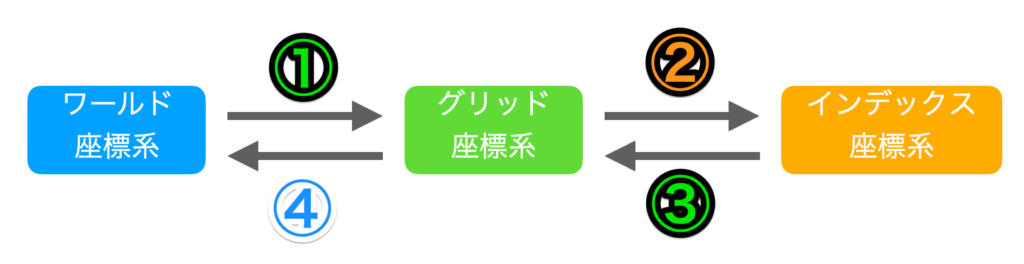
それぞれの計算式の例です。

①ワールド座標(wx, wy)をグリッド座標(gx, gy)に変換する

## ワールド座標系をグリッド座標系に変換する (X).
func world_to_grid_x(wx:float) -> int:
	# 左上のオフセット座標を引いてタイルサイズで割る
	var gx = int((wx - OFS_X) / TILE_SIZE)
	return gx

## ワールド座標系をグリッド座標系に変換する (Y).
func world_to_grid_y(wy:float) -> int:
	# 左上のオフセット座標を引いてタイルサイズで割る
	var gy = int((wy - OFS_Y) / TILE_SIZE)
	return gy

②グリッド座標をインデックス座標に変換する

## グリッド座標をインデックス座標に変換する.
func grid_to_idx(gx:int, gy:int) -> int:
	# グリッド座標(Y)のフィールドの横幅をかけて、グリッド座標(X)を足し込む
	return (gy * FIELD_WIDTH) + gx

③インデックス座標をグリッド座標に変換する


## インデックス座標をグリッドX座標に変換する.
func idx_to_grid_x(idx:int) -> int:
	# グリッド座標(X)はフィールドの横幅の剰余で求められる
	return idx % FIELD_WIDTH

## インデックス座標をグリッドY座標に変換する.
func idx_to_grid_y(idx:int) -> int:
	# グリッド座標(Y)はフィールドの横幅で割ることで求められる]
	return int(idx / FIELD_WIDTH)

④グリッド座標をワールド座標に変換する

## グリッド座標系をワールド座標系に変換する (X).
func idx_to_world_x(gx:int) -> float:
	var wx = OFS_X + (TILE_SIZE * gx)
	return wx

## グリッド座標系をワールド座標系に変換する (Y).
func idx_to_world_y(gy:int) -> float:
	var wy = OFS_Y + (TILE_SIZE * gy)
	return wy

ちなみにサンプルコードでは、グリッド座標系を「整数値」として扱いましたが、グリッド間の移動をなめらかにする場合には、グリッド座標系を小数値で扱ってしまって良いと思います。

例えば以下の記事で解説したマッチ3ゲームでは、グリッド座標系を小数値で処理しています。