今回はイージング関数を使ったUIの動きの作り方を紹介します。
イージング関数とは、
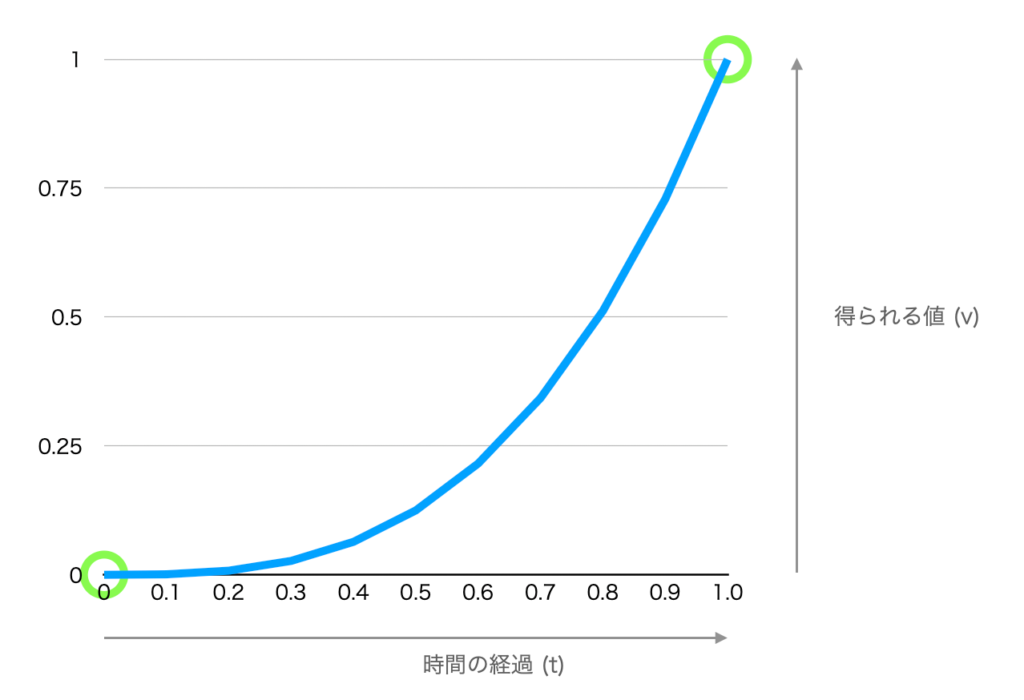
v = イージング関数(t) [t = 0.0〜1.0]
という式で表現され、t に “0.0〜1.0” の値を渡すといい感じの曲線で推移するパラメータを 0.0〜1.0 の範囲で返してくれる関数です。
UnityではDOTweenというアセットでイージング関数が実装されているので、Tweenという名称の方が馴染みがあるかもしれません。
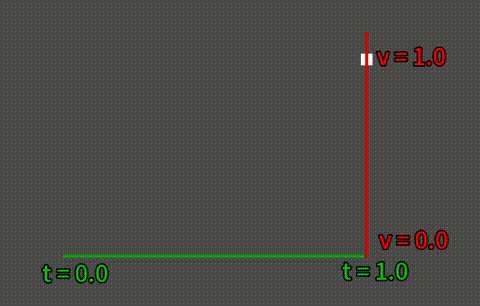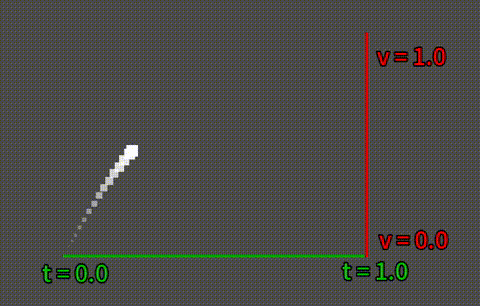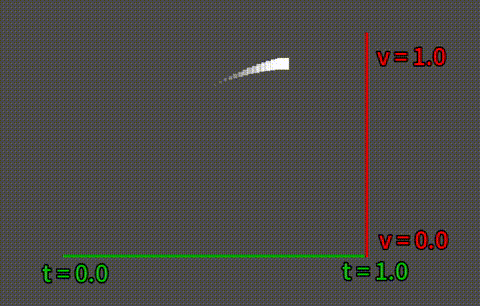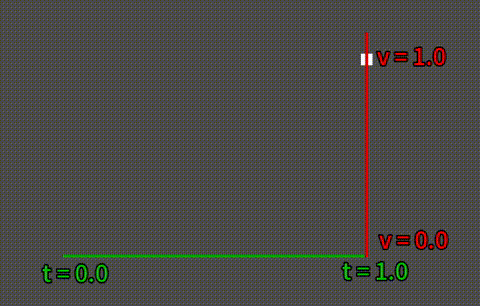
上記画像は、cubeOut (3次関数) によるイージング関数の使用例です。横軸が時間(t)の経過で、縦軸が値(v)の変化となります。
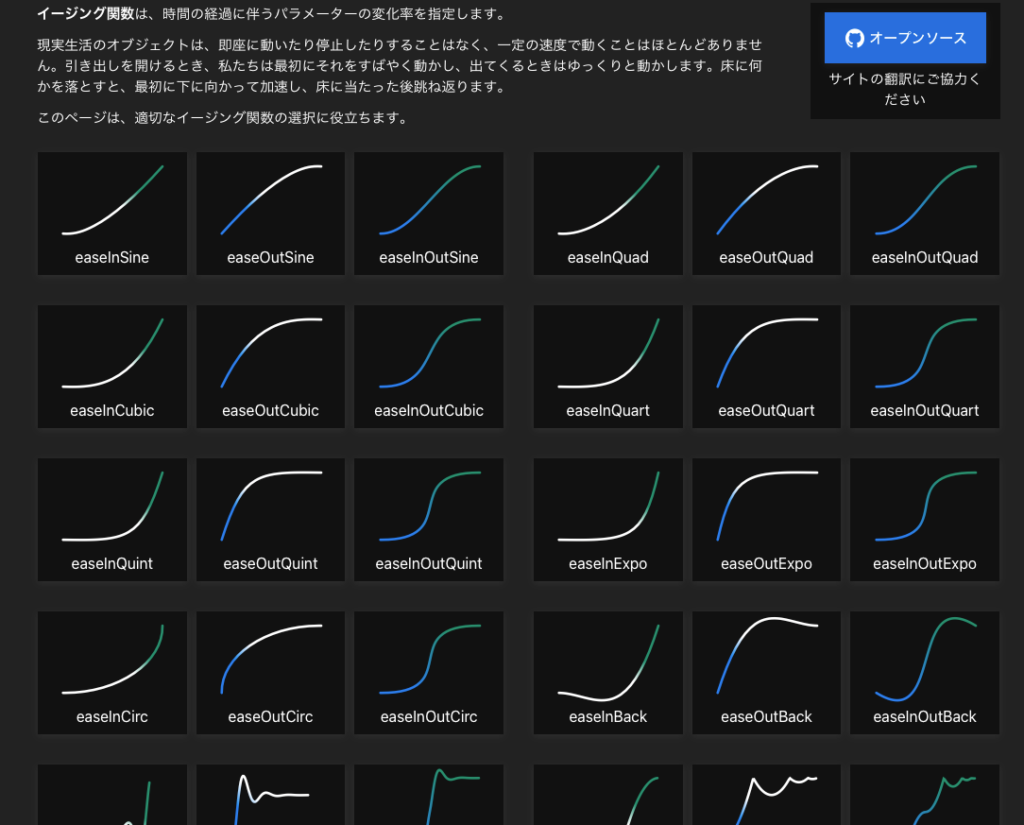
イージング関数の一覧は以下のページにまとめられています。
イージング関数が簡単に使用できるかどうかは環境によりますが、プログラムが書ければ移植は難しくありません。例えば、HaxeFlixelという開発環境ではcubeOutがこのような実装となっており、このコードを移植すればどの環境でもcubeOutを使用することができます。
// cubeOutのイージング関数
public static inline function cubeOut(t:Float):Float
{
return 1 + (--t) * t * t;
}例えばこれをPythonに移植したコードです。
def cubeIn(t):
return t * t * t
def cubeOut(t):
return 1 + (t - 1) * (t - 1) * (t - 1)いきなり cubeOutの紹介をしたので 3次関数のイメージがつきにくかったかもしれませんが、cubeInを見ると見慣れた3次関数 (y = x3) であることがわかります。
イージング関数の In と Out が登場したので、その違いをグラフで見てみます。
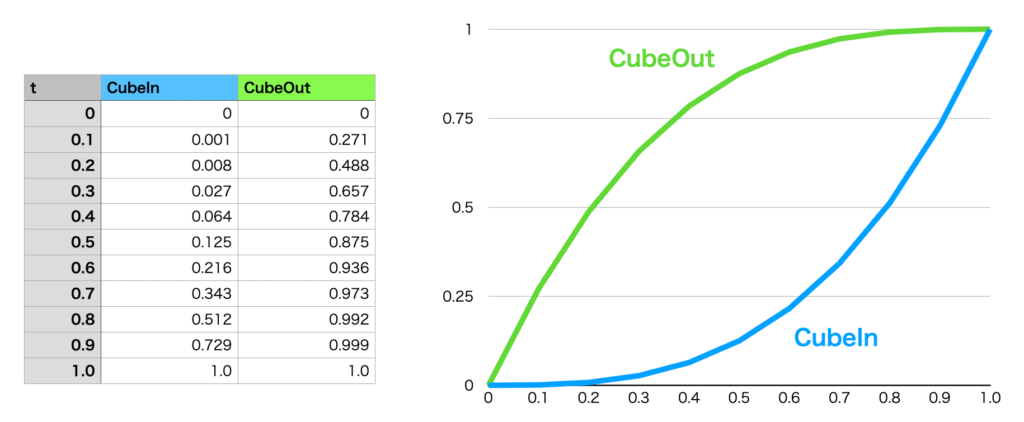
Inは見慣れた3次式のグラフです。それに対して、OutはInを中心を180度回転させたかのようなグラフとなります。なぜInとOutが存在するのかアニメーションでとても役に立つためなのですが、それについてはこの後解説します。
目次
イージング関数の使用例:テキストのスライドイン・スライドアウト
ここからイージング関数を使ってどのようなことができるのかを見ていきます。
さきほどの例で見たとおり、イージング関数には大きく分けて、山なりの動きをする Out 系、下側に膨らみのある In 系があります。そこで、この2つを連続して組み合わせると、ゲーム開始時のタイトルコール(テキスト)演出として、スライドイン・スライドアウトの動きを実装できます。

上記のテキストのスライドは、expoOut を1秒かけて再生し、完了後に expoIn を1秒かけて再生するようにしました。(expoは指数関数で、かなり急激な上昇をする関数となります)
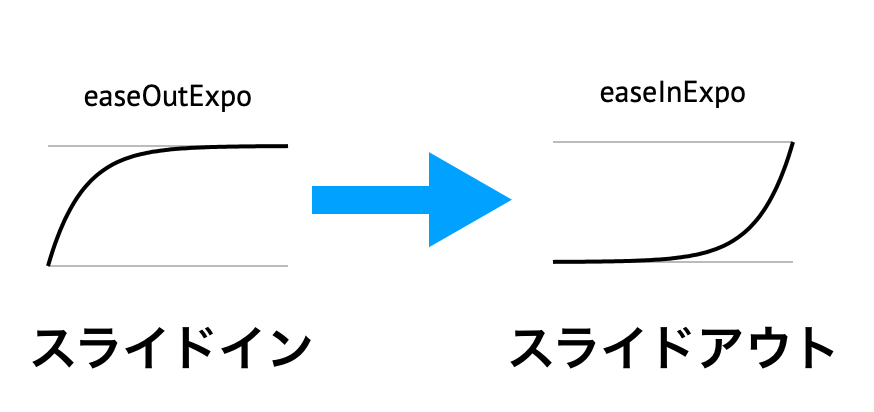
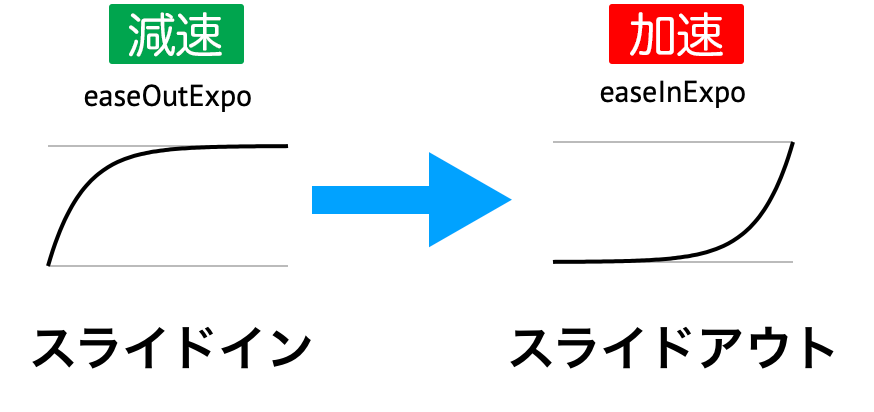
スライドインは Out を呼び出して、スライドアウトは In を呼び出す……? と用語が統一されず不思議に思ってしまいますが、Out は減速系、In は加速系と理解すればOKです
Outでスライドインするのはとても使い勝手が良いです。例えば、イージング関数を活用した例として、メニューの各項目の表示を Out で上から順に少しずらして登場させる使い方もあります。
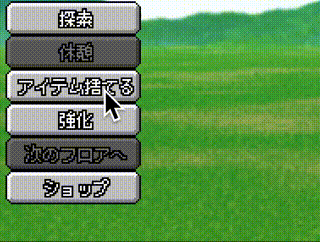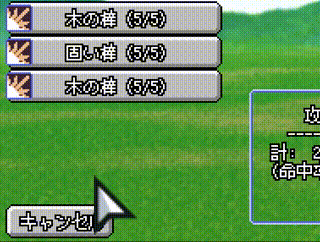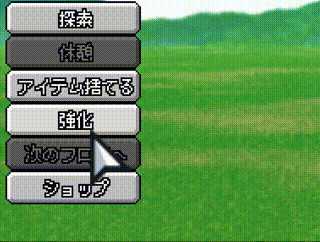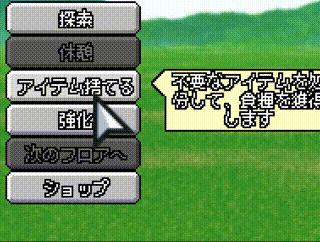
UIの動きに関するコツですが、各UIが同じ動きや速さで入場すると、「硬い」動きに見えてしまいます。

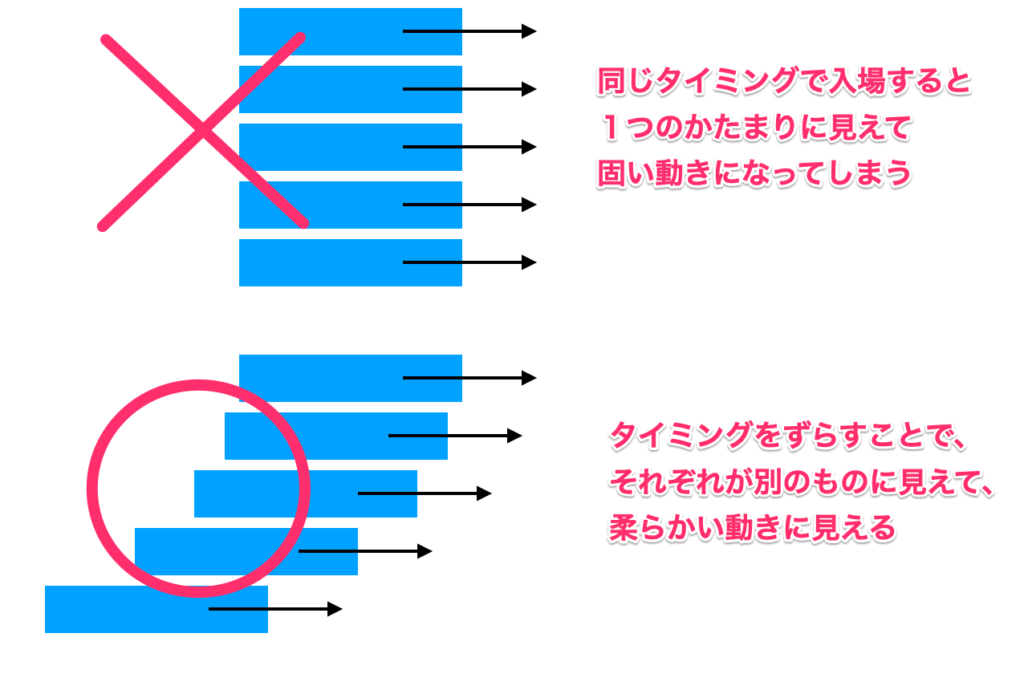
そこで、各UIをバラバラに(ディレイ)動かすと、柔らかい感じが出て、触っていて楽しいUIにすることができます。
それぞれのUIを少しずつズラして表示させたのが以下の例となります。

なお、頻繁に使うUIの入場は 0.5 秒ほどにしたほうがキレやテンポが良いと思います。


backOut は目的となる値を少しはみ出て戻ってくるイージング関数です。勢いよく出現して目標となる位置を少し通り過ぎて戻るような動きとなります。

この特性を使うと、若干コミカルにUIを登場させることが可能となります。そして退場するときには、同じbackOutを高速で逆再生移動させて退場させます。(通常 0.0→1.0 を渡すところを、逆再生では 1.0→0.0 とすると実装できます)
上記の例は、入場を 1秒とし、退場を 1 ÷ 3 = 0.333 秒(3分の1の時間なので3倍速)としました。UIは入場を速くしすぎると何が起きているかわからなくなるので、ある程度視認できる速さにしますが、退場する場合は「そのUIはもう不要となった」ので、高速で退場させた方が、次のステップに早く進むことでテンポが良くなり、ユーザビリティが上昇します。場合によっては退場アニメーションはなしで、パッと消してしまっても問題ないです。

ElasticOut を使うとカードGET的なぼよよん演出を実装できます。
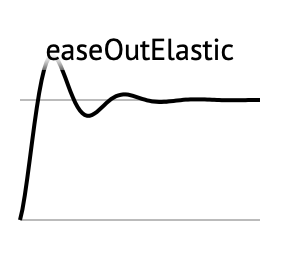
例で適用しているのは、画像のスケール値(拡大縮小値)です。おおよそ 1.0秒〜1.5秒にするとシュッと登場して良いでしょう。

複数のUIに ElasticOut をかけてバラバラに出現させるのも良いです。
イージング関数を使う・使わないに限らず、UIの動きをつけるときに気をつけると良いポイントは以下の通りです。
- 線形(等速)の動きは固く見えてしまうので、可能な限り曲線を使う
- 各UIは動きを少しバラす(開始タイミングをずらす)と動きが柔らかくなる
- UIが退場する場合は、高速で退場しても構わない(パッと消えても構わない)
さらに高度なテクニックとして、あるUIの退場の途中で別のUIを入場させる「クロスフェード」もしくは「シームレス」で重ねる方法もあります。ただ、この方法は状態遷移や管理が少し厄介です。プログラムに自信があれば実装してみるのも良いと思います。
また、イージング関数については、より理解を深めたい場合には以下の動画もオススメです。
なんだかお笑い芸人のような二人ですが、ちゃんとしたインディーゲーム開発者です。イージング関数を使うことでシンプルなブロック崩しがここまでジューシーに(面白そうに)見えるんだよ、という例の紹介です。
今回の記事では、UIの移動と拡大のみを紹介しましたが、この動画では、イージング関数の別の用途を解説しています。
- アニメーション: キャラクター・UIの移動、拡大縮小、回転、フェード
- トランジション: 場面転換、入場、退場
- ディレイ: 演出開始の遅延
イージング関数から少し離れますが、UIの作り込みが最もスゴイのがペルソナ5のキャンプUIです。
動きのかっこよさが目立ちますが、UIとしての「わかりやすさ」と「操作感の良さ」を共存させているのがスゴイです。色々動いているのですが、操作対象をしっかり目立たせることちゃんと視線誘導できているのですよね。また「各画面をシームレスにつなぐ」という面倒なこともしっかりやっています。
C+での実装例
イージング関数の実装例は調べるといくつか見つかるので、もし使用している環境で実装されていない場合はそれを参考にすると良いと思います。例えば、C++での実装であれば、「イージング関数を使いたい@C++」というページが参考になります。

この動きはPyxelで実装したものです。
import pyxel
import math
# Elastic関数
def easeOutElastic(t):
ELASTIC_AMPLITUDE = 1
ELASTIC_PERIOD = 0.4
return (ELASTIC_AMPLITUDE * math.pow(2, -10 * t) * math.sin((t - (ELASTIC_PERIOD / (2 * math.pi) * math.asin(1 / ELASTIC_AMPLITUDE))) * (2 * math.pi) / ELASTIC_PERIOD) + 1)
# 指数関数
def easeOutExpo(t):
return -math.pow(2, -10*t) + 1
# バック関数
def easeOutBack(t):
return 1 - (t - 1) * (t-1) * (-2.70158 * (t-1) - 1.70158)
# UIオブジェクト
class Obj:
RECT = 1
CIRCLE = 2
def __init__(self, x, y, text, type):
# 初期化
self.x = x
self.y = y
self.tx = x
self.ty = y
self.timer = 0
self.max = 0
self.delay = 0
self.text = text
self.type = type
def start(self, tx, ty, timer):
# 開始
self.delay = 0
self.timer = 0
self.max = timer
self.tx = tx
self.ty = ty
def update(self):
# 更新
if self.delay > 0:
# ディレイ中
self.delay -= 1
return
if self.timer < self.max:
self.timer += 1
else:
self.x = self.tx
self.y = self.ty
def draw(self):
if self.delay > 0:
# ディレイ中なので描画しない
return
dx = self.tx - self.x
dy = self.ty - self.y
rate = self.timer / self.max
if self.type == self.RECT:
# メニュは指数関数の動き
rate = easeOutExpo(rate)
elif self.type == self.CIRCLE:
# 丸はElastic関数
rate = easeOutElastic(rate)
#rate = easeOutBack(rate)
px = self.x + (dx * rate)
py = self.y + (dy * rate)
if self.type == self.RECT:
# メニューの描画
pyxel.rect(px, py, px+40, py+8, 7)
pyxel.text(px+2, py+2, self.text, 0)
elif self.type == self.CIRCLE:
# 円の描画
size = 12
d = size * rate
pyxel.circ(self.x, self.y, d, 9)
class App:
def __init__(self):
pyxel.init(160, 120, fps=60)
self.init()
pyxel.run(self.update, self.draw)
def init(self):
self.objs = []
# メニュー
txts = [
"Attack",
"Skill",
"Item",
"Defense",
"Escape"
]
for i, text in enumerate(txts):
px = -100
py = 4 + i * 12
obj = Obj(px, py, text, Obj.RECT)
self.objs.append(obj)
# 表示開始
obj.start(8, py, 60)
obj.delay = i * 5
# 丸の表示
for i in range(3):
px = 70 + i * 32
py = 32
obj = Obj(px, py, "", Obj.CIRCLE)
self.objs.append(obj)
# 表示開始
obj.start(px, py, 90)
obj.delay = 30 + i * 13
def update(self):
if pyxel.btnp(pyxel.KEY_R):
self.init()
for obj in self.objs:
obj.update()
def draw(self):
pyxel.cls(0)
for obj in self.objs:
obj.draw()
App()またイージング関数について、HaxeFlixelのコード
https://github.com/HaxeFlixel/flixel/blob/dev/flixel/tweens/FlxEase.hx
を参考にPythonへ移植してみました。
import math
# 一次関数
def linear(t):
return t
# 二次関数
def quadIn(t):
return t * t
def quadOut(t):
return -t * (t - 2)
def quadInOut(t):
if t <= 0.5:
return t * t * 2
else:
return 1 - (t - 1) * (t - 1) * 2
# 三次関数
def cubeIn(t):
return t * t * t
def cubeOut(t):
return 1 + (t - 1) * (t - 1) * (t - 1)
def cubeInOut(t):
if t <= 0.5:
return t * t * t * 4
else :
return 1 + (t - 1) * (t - 1) * (t - 1) * 4
# 四次関数
def quartIn(t):
return t * t * t * t
def quartOut(t):
return 1 - (t - 1) * (t - 1) * (t - 1) * (t - 1)
def quartInOut(t):
if t <= 0.5:
return t * t * t * t * 8
else:
t = t * 2 - 2
return (1 - t * t * t * t) / 2 + 0.5
# 五次関数
def quintIn(t):
return t * t * t * t * t
def quintOut(t):
t = t - 1
return t * t * t * t * t + 1
def quintInOut(t):
t *= 2
if (t < 1):
return (t * t * t * t * t) / 2
else:
t -= 2
return (t * t * t * t * t + 2) / 2
# スムーズ曲線
def smoothStepIn(t):
return 2 * smoothStepInOut(t / 2)
def smoothStepOut(t):
return 2 * smoothStepInOut(t / 2 + 0.5) - 1
def smoothStepInOut(t):
return t * t * (t * -2 + 3)
# よりスムーズな曲線
def smootherStepIn(t):
return 2 * smootherStepInOut(t / 2)
def smootherStepOut(t):
return 2 * smootherStepInOut(t / 2 + 0.5) - 1
def smootherStepInOut(t):
return t * t * t * (t * (t * 6 - 15) + 10)
# SIN関数(0〜90度)
def sineIn(t):
return -math.cos(math.pi/2 * t) + 1
def sineOut(t):
return math.sin(math.pi/2 * t)
def sineInOut(t):
return -math.cos(math.pi * t) / 2 + .5
# バウンス関数
def bounceIn(t):
B1 = 1 / 2.75
B2 = 2 / 2.75
B3 = 1.5 / 2.75
B4 = 2.5 / 2.75
B5 = 2.25 / 2.75
B6 = 2.625 / 2.75
t = 1 - t
if (t < B1): return 1 - 7.5625 * t * t
if (t < B2): return 1 - (7.5625 * (t - B3) * (t - B3) + .75)
if (t < B4): return 1 - (7.5625 * (t - B5) * (t - B5) + .9375)
return 1 - (7.5625 * (t - B6) * (t - B6) + .984375)
def bounceOut(t):
B1 = 1 / 2.75
B2 = 2 / 2.75
B3 = 1.5 / 2.75
B4 = 2.5 / 2.75
B5 = 2.25 / 2.75
B6 = 2.625 / 2.75
if (t < B1): return 7.5625 * t * t
if (t < B2): return 7.5625 * (t - B3) * (t - B3) + .75
if (t < B4): return 7.5625 * (t - B5) * (t - B5) + .9375
return 7.5625 * (t - B6) * (t - B6) + .984375
def bounceInOut(t):
B1 = 1 / 2.75
B2 = 2 / 2.75
B3 = 1.5 / 2.75
B4 = 2.5 / 2.75
B5 = 2.25 / 2.75
B6 = 2.625 / 2.75
if (t < .5):
t = 1 - t * 2
if (t < B1): return (1 - 7.5625 * t * t) / 2
if (t < B2): return (1 - (7.5625 * (t - B3) * (t - B3) + .75)) / 2
if (t < B4): return (1 - (7.5625 * (t - B5) * (t - B5) + .9375)) / 2
return (1 - (7.5625 * (t - B6) * (t - B6) + .984375)) / 2
else:
t = t * 2 - 1
if (t < B1): return (7.5625 * t * t) / 2 + .5
if (t < B2): return (7.5625 * (t - B3) * (t - B3) + .75) / 2 + .5
if (t < B4): return (7.5625 * (t - B5) * (t - B5) + .9375) / 2 + .5
return (7.5625 * (t - B6) * (t - B6) + .984375) / 2 + .5
# 円
def circIn(t):
return -(math.sqrt(1 - t * t) - 1)
def circOut(t):
return math.sqrt(1 - (t - 1) * (t - 1))
def circInOut(t):
if t <= .5:
return (math.sqrt(1 - t * t * 4) - 1) / -2
else:
return (math.sqrt(1 - (t * 2 - 2) * (t * 2 - 2)) + 1) / 2
# 指数関数
def expoIn(t):
return math.pow(2, 10 * (t - 1))
def expoOut(t):
return -math.pow(2, -10*t) + 1
def expoInOut(t):
if t < .5:
return math.pow(2, 10 * (t * 2 - 1)) / 2
else:
return (-math.pow(2, -10 * (t * 2 - 1)) + 2) / 2
# バック
def backIn(t):
return t * t * (2.70158 * t - 1.70158)
def backOut(t):
return 1 - (t - 1) * (t-1) * (-2.70158 * (t-1) - 1.70158)
def backInOut(t):
t *= 2
if (t < 1):
return t * t * (2.70158 * t - 1.70158) / 2
else:
t -= 1
return (1 - (t - 1) * (t - 1) * (-2.70158 * (t - 1) - 1.70158)) / 2 + .5
# 弾力関数
def elasticIn(t):
ELASTIC_AMPLITUDE = 1
ELASTIC_PERIOD = 0.4
t -= 1
return -(ELASTIC_AMPLITUDE * math.pow(2, 10 * t) * math.sin( (t - (ELASTIC_PERIOD / (2 * math.pi) * math.asin(1 / ELASTIC_AMPLITUDE))) * (2 * math.pi) / ELASTIC_PERIOD))
def elasticOut(t):
ELASTIC_AMPLITUDE = 1
ELASTIC_PERIOD = 0.4
return (ELASTIC_AMPLITUDE * math.pow(2, -10 * t) * math.sin((t - (ELASTIC_PERIOD / (2 * math.pi) * math.asin(1 / ELASTIC_AMPLITUDE))) * (2 * math.pi) / ELASTIC_PERIOD) + 1)
def elasticInOut(t):
#ELASTIC_AMPLITUDE = 1
ELASTIC_PERIOD = 0.4
if (t < 0.5):
t -= 0.5
return -0.5 * (math.pow(2, 10 * t) * math.sin((t - (ELASTIC_PERIOD / 4)) * (2 * math.pi) / ELASTIC_PERIOD))
else:
t -= 0.5
return math.pow(2, -10 * t) * math.sin((t - (ELASTIC_PERIOD / 4)) * (2 * math.pi) / ELASTIC_PERIOD) * 0.5 + 1今回の記事を動画にしました


