1.はじめに
今回はリバーシの作り方を解説します。
リバーシは、プログラム初心者でも簡単に作れるわりに、盤面の扱い・CPUの思考ルーチンなどにこだわれば、凝ったプログラムができる、なかなか面白い題材です。
2.盤面の設計
まず、リバーシの盤面の設計をします。クラス図としてはこんな感じです。
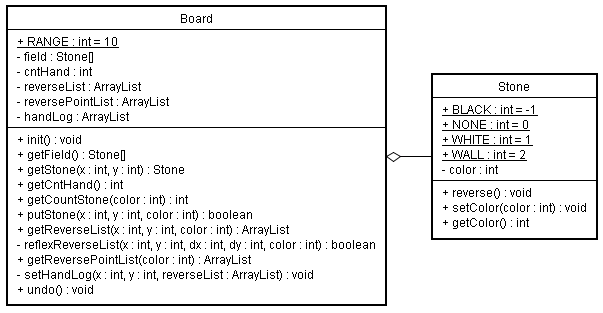
石であるStoneクラスを見てみます。属性としては、とりあえず「色」の属性があれば充分です。(ひっくり返した場合に飛び跳ねるような処理を行いたい場合には、座標の情報などが必要になります)
他に、スタティックな属性として、
- BLACK
- NONE
- WHITE
- WALL
というものを持っています。
ポイントは、BLACKが「-1」でWHITE「1」となっているところです。これは、reverseメソッドなどで石を反転させる場合、-1をかけるだけでよいため、このようにしています。
もう一つのポイントとしては、WALL属性です。盤面クラス(Boardクラス)のfield属性が、盤面の情報となるのですが、サイズ(RANGE属性)を「10」としています。
これは、盤面のサイズを、本来のサイズである「8」にしてしまうと、盤面探索時に配列オーバーを起こしてしまいます。
そのため、周りに1つ壁を作っているわけです。
さて、続いて盤面である、Boardクラスを見てみます。RANGE、field属性については、先ほど説明したとおり、盤面の石の配置状態を持っています。initメソッド呼び出し時に、Stoneクラスのインスタンスを作り、fieldを初期化します。
cntHand属性は、現在の手数となります。リバーシでは60手を超えると、盤面が全て石で埋まりますので、こういったものがあると何かと便利ですよね。
getCountStoneメソッドは、指定した色がどれだけあるかを返します。putStoneメソッドは、座標と色を指定して、石を置きます。
さて、ここからが盤面クラスのポイントです。まず、getReverseListメソッドですが、座標と色を指定すると、「ひっくり返すことができる石の座標のリスト」を返します。
putStoneメソッドの中で、このgetReverseListメソッドを呼び出し、その結果に基づき、石をひっくり返すようにします。
なぜこのようにgetReverseListメソッドを独立させているのかというと、盤面にひっくり返すことができる数を表示させたり、CPUの思考ルーチンに必要となるからです。
getReverseListメソッドの中では、再帰関数reflexReverseListメソッドを呼び出します。なぜ再帰処理にしているのかというと、ひっくり返すことを探索する場合には、以下の処理を行うためです。
x,yに黒石を置いたとします。この場合、8方向に探索を行うのですが、これには一定のパターンがあります。
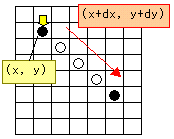
- 指定した方向に探索し続ける
- 探索場所が黒石*-1であれば探索を続ける
- 探索場所が黒石であればそれまでにはさんだ黒石*-1をひっくり返すことができる
- 探索場所が黒石かつ黒石*-1でもない場合、その方向にひっくり返す石はない
1については、基点となる(x,y)に移動量(dx,dy)を足しこんでいくことで実装します。
2については、探索を続けるのですから、再帰関数を呼び続けることになりますよね。そして、その戻り値がtrueであれば、reverseListに現在の座標を追加します。
3は、戻り値をtrueにすることで、呼び出し元がひっくり返すことできることを教えます。
4は、ひっくり返すことができないので、戻り値がfalseになります。
とまあ、再帰処理に慣れていない人にはナンノコトヤラですが…。繰り返しの処理を行う場合に再帰処理を使うと、すっきりしたコードを書くことができる場合があります。
ですが、再帰処理は普通のループ文と条件式で置き換えることができますので、理解できなかった場合は、その方法で書いたほうがいいかもしれません。
また、再帰処理は、関数呼出しごとにスタックにメモリを積んでいくので、パフォーマンスが落ちます。ですから、スピードが必要な処理の場合は、普通に書いたほうがいいかもしれません。
さて、もう一つのポイントgetReversePointListメソッドです。これは、指定した色を置くことができる座標のリストを返します。これにより、ひっくり返すことができる場所を表示したり、CPUの思考ルーチンを楽に作ることができます。
最後にundoメソッドです。これは、進めた手を戻す処理です。なぜこの処理が必要なのかというと、CPUの思考ルーチンの「先読み」処理を作る場合に必要となるからです。
例えば、3手先まで読む場合には、実際に石を置いて盤面を3手先まで進める、といった処理を行うため、思考ルーチンが終了した場合には、手を戻す必要があるからです。
盤面の設計は以上です。CPUの思考ルーチンはランダムに置くというだけでも、ゲームはできますので、ここまでできれば、一応、完成ですね。
3.CPUの思考ルーチン
CPUの思考ルーチンについて解説します。クラス設計としては、以下のようになります。
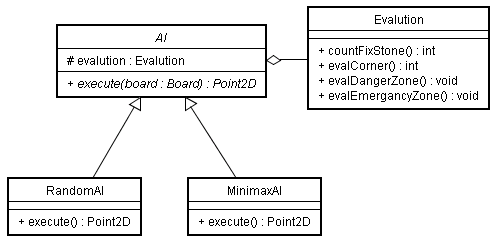
executeメソッドを継承したクラスで実装するという、
典型的なストラテジーパターンですね。Evalutionクラスは、手や盤面の評価を行うクラスです。
では、思考ルーチンの基本ともいえる、ミニマックス法について解説します。まずはこの図を見てください。
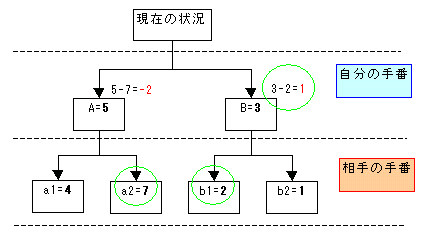
この図では、自分の選ぶことができる手として、AとBがあります。Aを選ぶと評価としては「+5」、Bを選ぶと評価としては「+3」です。自分の番だけ考えれば、Aを選ぶべきです。
しかし、ここでは次に相手がどんな手を打つかを「先読み」してみます。Aを選ぶと相手にはa1とa2があります。a1は「+4」a2は「+7」です。相手が十分に賢いと仮定すると、a2を選択します。
こうすると、相手にとってのプラスは自分にとってのマイナスですから、Aの評価は、「5-7=-2」となります。それに対して、Bを選択すると、相手はb1を選択しますから、Bの評価は、「3-2=1」となります。
よって、Bを選択する方が、評価は高いことになります。
このように、自分はMaximumとなる評価、相手は自分にとってMinimumとなる評価、を選択することから、ミニマックス法、と呼びます。
では、この「評価」の値を計算するにはどうすればいいのでしょうか。実はこっちの方が重要だったりします。
方針としては、例えば以下のものがあります。
- ひっくり返すことのできる石の数
- 角に置く
- 置く場所が危険地帯
- 置くと「確定石」が増える
- 置くと「着手点」が多くなる
- 開放度
1は真っ先に思いつくと思います。
ゲームの終盤ではたくさんの石をひっくり返すべきですし、全滅を狙うためにも必要です。しかし、少しでもリバーシをやったことがある人には、単純に多く取ればいいものではないことは知ってますよね。むしろ、「角に置く手」が重要ですよね。そして、逆に「相手に角を取られるような手」は危険です。
2の「角に置く」手には高い評価を与えます。
3の「置く場所が危険地帯(角を取られてしまうような場所)」の手にはマイナスの評価を与えます。これだけでもそれなりに強いですが、さらに強くするためには、以下の評価を考慮します。
4の「確定石」とは、相手にひっくり返されない自分の石のことです。例えば、角は相手に返されません。また、角に隣接する石も相手に返されません。こういった石が増える手は高く評価します。
あと、強い人なら、以下の状況は有利であることを知っています。
- 置くことができる場所(着手点)が多い
- 自分の石の周りが相手の石に囲まれている(開放度が低い)
余裕があれば、こういった評価も行います。
評価の方針としては、以上です。
ということで、評価をいくつにするか、ということですが、これに答えはありません。
ここら辺は作る人の個性が出るところですね。
例えば、角に辛くするなら、角に置く手の評価を高くしたりと、まあ、、、実際にゲームをしながら、数値をいじってみるのが一番です。(個人的には、このバランス調整の作業が一番面白かったりします
最後に、、もっと処理にこだわると、α-β法や評価のテーブル化など、処理を軽くすることができたりします。処理を軽くすれば、もっと先の手を読んでもプレイに差支えがないので、さらに強い思考ルーチンが作れますよね。
ちなみに参考書籍としてはこちらです。
思考ルーチンについてかなりマニアックに書かれていてオススメです。