今回は重み付けの確率計算の方法について解説します。
目次
確率の計算方法
重み付けの説明の前に、基本的な確率計算の方法について確認しておきます。
まずは、サイコロで1の目が出る確率の求め方です。
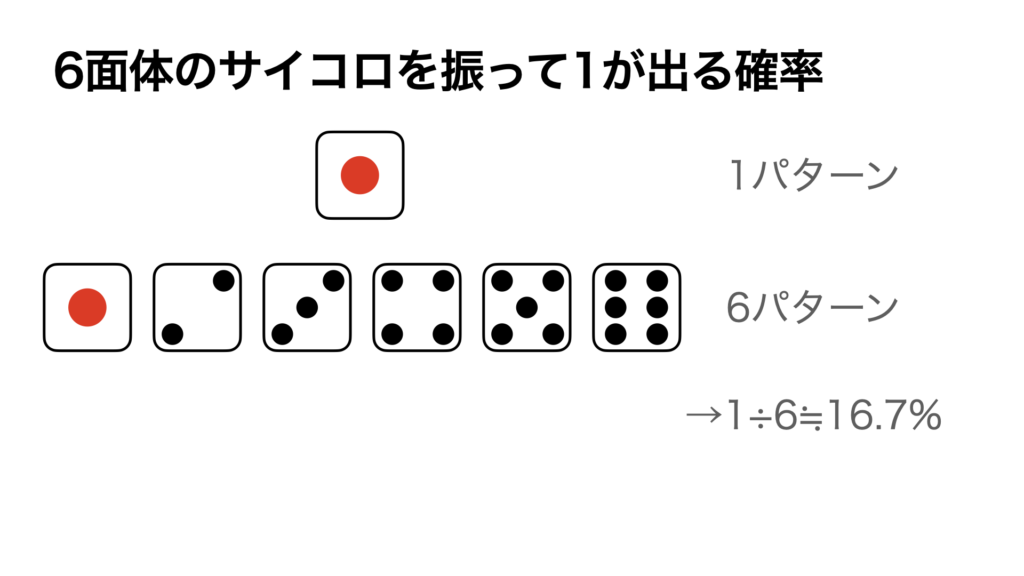
6面体のサイコロは6通りのパターンがあり、それぞれが均等の確率で出現します。
そして、1の目は1つのみ存在します。
そのため、6通りのうちの1つが出る確率を求めることとなり、
1÷6≒16.7% となります。
次に、サイコロで3の倍数が出る確率を求めます。
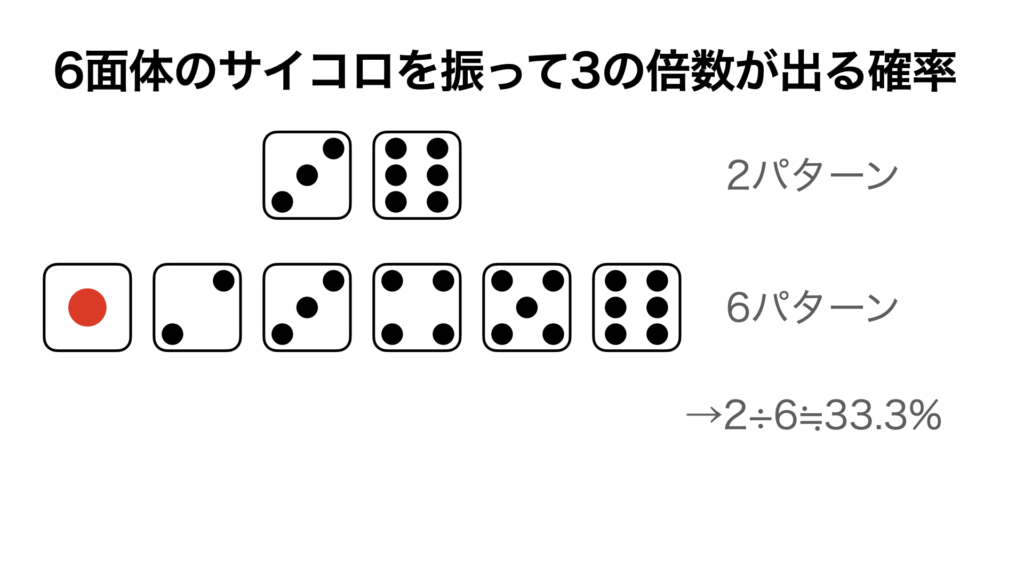
3の倍数は、3と6の2つあります。
そのため、6通りのうち2パターンの目が出る確率を求めることとなり、
2÷6≒33.3% となります。
ここまでの例でわかるように、確率を求めるための法則は、
「組み合わせの数」÷「組み合わせの総数」という式となります。

くじ引きの確率を求める
基本がわかったところで、くじ引きの抽選確率を求めてみます。

このくじ引きは、A賞の当たりが1本、B賞の当たりが3本、C賞の当たりが10本……という偏りのある抽選です。
この場合、各賞の確率はどのように求めるのでしょうか。
まず先程の式「組み合わせの数」÷「組み合わせの総数」を思い出します。
このくじでの「組み合わせの数」は各賞の当たりの本数です。
これが分子となります。
そして分母となる「組み合わせの総数」はA賞、B賞、C賞の当たり本数の合計となります。
ですので、1+3+10=14
となり、14が分母となります。
そして各賞の当たり本数を分子にもってくることで確率が求められます。

- A賞の確率は1÷14で約7.1%。
- B賞の確率は3÷14で約21.4%。
- C賞の確率は10÷14で約71.4%
となります。
重み付け抽選をプログラムへ落とし込む
では、この考え方をプログラムに落とし込むにはどのように書くか……ということについて説明します。
たいていのプログラムには rand関数が用意されており、これを使うことで一定の範囲の乱数を得ることができます。
例えば、これはサイコロの 1〜6 の値を得る、C言語のプログラムです。
// rand()%6で0~5がランダムで得られる
// ので +1 して 1〜6にする
int dice = (rand()%6) + 1;では、先程のくじ引きをプログラムで書くにはどのように考えるのか……?
それはこのように考えます。
組み合わせの総数は14です。すなわち、
// rndには 0〜13 の値が入る
int rnd = rand()%14;このようにすると、14パターンの乱数を得ることができます。
それをこのように割り振って判定します。
| 当たりとなる賞 | 当たり本数 | 乱数の値 |
|---|---|---|
| A賞 | 1本 | 0 |
| B賞 | 3本 | 1〜3 |
| C賞 | 10本 | 4〜13 |
A賞は「0」のみが当たりとなります。
そしてB賞は「1、2、3」が当たりとなります。
最後にC賞は「4から13」を当たりとします。
よりプログラム的な説明をすると、このような判定となります。
0〜13の乱数値rndと各賞の当たりの本数を順に比較していきます。
条件を満たせばその賞を返し、満たさない場合はrndから当たり本数を引くことで、次の当たり本数との比較ができるようになります。
言葉だけだと少しむずかしいかもしれないので、実際にC言語のコードで説明をします。
/**
* 重み付けで抽選を行う
* @param pArray 抽選する対象の配列
* @param Length 配列のサイズ
* @return 抽選結果(配列の要素)
*/
int WeightedPick(int* pArray, int Length) {
int totalWeight = 0;
int pick = 0;
// トータルの重みを計算する
for(int i = 0; i < Length; i++) {
totalWeight += pArray[i];
}
// 抽選する
int rnd = rand()%totalWeight;
for(int i = 0; i < Length; i++) {
if(rnd < pArray[i]) {
// 抽選対象決定
pick = i;
break;
}
// 次の対象を調べる
rnd -= pArray[i];
}
return pick;
}
この関数は、抽選対象の配列を引数として受け取り、抽選結果を配列の要素番号で返すものとなります。
まずはトータルの重みの計算を行います。
引数で渡された配列の合計を求めます。
次に、rand関数で抽選を行います。
そして抽選結果の要素番号を返す処理となります。
先ほど説明したとおり、rnd変数の値と当たり本数を比較し、ハズレの場合は当たり本数で引くことにより、次の判定を行う値となります。
重み付けの抽選を行うメリット
以上、重み付けの抽選を行うアルゴリズムの解説をしました。
最後にこれを使うことで、どういったメリットがあるのかを、具体的な例で説明します。
結論を先にいうと「ローグライク」のような乱数が中心となるゲームを作るときに役に立ちます。
ローグライクは一般的には「自動生成されるダンジョン」のイメージが強いですが、ゲームメカニクスのコアは乱数の不安定な揺らぎで変化する敵やアイテムをプレイヤーのスキルで乗り越えていくところにあると考えています。
その中の1つの要素として、ゲームの進行に合わせて変化するアイテムドロップがあります。
例えばアイテムドロップの出現ルールをこのように定義します。
| アイテム名 | 登場ステージ | 重み |
|---|---|---|
| 薬草 | 1〜5 | 100 |
| 木の棒 | 1〜5 | 50 |
| こん棒 | 1〜5 | 10 |
| 毒消し草 | 2〜5 | 30 |
| 銅の剣 | 3〜5 | 2 |
薬草、木の棒、こん棒はすべてのステージでドロップします。
毒消し草はステージ2から登場します。
そして銅の剣はステージ3から登場します。
このように定義した場合、
ステージ1で出現するアイテムとそのドロップ率をまとめたのがこちらです。
- 薬草: 100÷160≒62.50%
- 木の棒: 50÷160≒31.25%
- こん棒: 10÷160≒6.25%
出現するアイテムの重みの合計を求め、それを分母にしてそれぞれの重みで按分することでそれぞれのドロップ率が計算できます。
次にステージ2です。
毒消し草が追加されるので、それを加えたのがトータルの重みとなり、それぞれのドロップ率が計算できます。
- 薬草: 100÷190≒52.63%
- 木の棒: 50÷190≒26.32%
- こん棒: 10÷190≒5.26%
- 毒消し草: 30÷190≒15.79%
最後にステージ3以降です。
銅の剣が追加されました。
- 薬草: 100÷192≒52.08%
- 木の棒: 50÷192≒26.04%
- こん棒: 10÷192≒5.21%
- 毒消し草: 30÷190≒15.63%
- 銅の剣: 2÷192≒1.04%
このように、動的に抽選対象が増えるようなゲームの場合、このような重み付けの抽選がとても役に立ちます。
まとめ
以上、重み付けの抽選アルゴリズムを紹介しました
- 重み付けの抽選は、各抽選対象に重みの数値を指定する
- それぞれの当たりの確率は重みの合計を分母にすることで求められる
- 抽選対象が動的に増えるゲームで役に立つ
YouTube
今回記事にした内容を動画にしたものです。


