Godotでは Tween というイージング関数を使ったアニメーションノードが実装されていますが、よりお手軽に使えるようにしたものを公開しておきます。
イージング関数のサンプルコード
以下のスクリプトを Ease.gd として保存し、プロジェクトに追加します。
extends Node2D
# ===================================
# イージング関数定義
# ===================================
class_name Easing
enum eType {
LINEAR, # 線形
QUAD_IN, # 二次関数
QUAD_OUT,
QUAD_INOUT,
CUBE_IN, # 三次関数
CUBE_OUT,
CUBE_INOUT,
QUART_IN, # 四次関数
QUART_OUT,
QUART_INOUT,
QUINT_IN, # 五次関数
QUINT_OUT,
QUINT_INOUT,
SMOOTH_STEP_IN, # スムーズ曲線
SMOOTH_STEP_OUT,
SMOOTH_STEP_INOUT,
SMOOTHER_STEP_IN, # よりスムーズな曲線
SMOOTHER_STEP_OUT,
SMOOTHER_STEP_INOUT,
SIN_IN, # SIN関数
SIN_OUT,
SIN_INOUT,
BOUNCE_IN, # バウンス
BOUNCE_OUT,
BOUNCE_INOUT,
CIRC_IN, # サークル
CIRC_OUT,
CIRC_INOUT,
EXPO_IN, # 指数関数
EXPO_OUT,
EXPO_INOUT,
BACK_IN, # バック
BACK_OUT,
BACK_INOUT,
ELASTIC_IN, # 弾力関数
ELASTIC_OUT,
ELASTIC_INOUT,
}
# 一次関数
func linear(t:float) -> float:
return t
# 二次関数
func quad_in(t:float) -> float:
return t * t
func quad_out(t:float) -> float:
return -t * (t - 2)
func quad_in_out(t:float) -> float:
if t <= 0.5:
return t * t * 2
else:
return 1 - (t - 1) * (t - 1) * 2
# 三次関数
func cube_in(t:float) -> float:
return t * t * t
func cube_out(t:float) -> float:
return 1 + (t - 1) * (t - 1) * (t - 1)
func cube_in_out(t:float) -> float:
if t <= 0.5:
return t * t * t * 4
else :
return 1 + (t - 1) * (t - 1) * (t - 1) * 4
# 四次関数
func quart_in(t:float) -> float:
return t * t * t * t
func quart_out(t:float) -> float:
return 1 - (t - 1) * (t - 1) * (t - 1) * (t - 1)
func quart_in_out(t:float) -> float:
if t <= 0.5:
return t * t * t * t * 8
else:
t = t * 2 - 2
return (1 - t * t * t * t) / 2 + 0.5
# 五次関数
func quint_in(t:float) -> float:
return t * t * t * t * t
func quint_out(t:float) -> float:
t = t - 1
return t * t * t * t * t + 1
func quint_in_out(t:float) -> float:
t *= 2
if (t < 1):
return (t * t * t * t * t) / 2
else:
t -= 2
return (t * t * t * t * t + 2) / 2
# スムーズ曲線
func smooth_step_in(t:float) -> float:
return 2 * smooth_step_in_out(t / 2)
func smooth_step_out(t:float) -> float:
return 2 * smooth_step_in_out(t / 2 + 0.5) - 1
func smooth_step_in_out(t:float) -> float:
return t * t * (t * -2 + 3)
# よりスムーズな曲線
func smoother_step_in(t:float) -> float:
return 2 * smoother_step_in_out(t / 2)
func smoother_step_out(t:float) -> float:
return 2 * smoother_step_in_out(t / 2 + 0.5) - 1
func smoother_step_in_out(t:float) -> float:
return t * t * t * (t * (t * 6 - 15) + 10)
# SIN関数(0〜90度)
func sine_in(t:float) -> float:
return -cos(PI/2 * t) + 1
func sine_out(t:float) -> float:
return sin(PI/2 * t)
func sine_in_out(t:float) -> float:
return -cos(PI * t) / 2 + .5
# バウンス関数
const B1 = 1 / 2.75
const B2 = 2 / 2.75
const B3 = 1.5 / 2.75
const B4 = 2.5 / 2.75
const B5 = 2.25 / 2.75
const B6 = 2.625 / 2.75
func bounce_in(t:float) -> float:
t = 1 - t
if (t < B1): return 1 - 7.5625 * t * t
if (t < B2): return 1 - (7.5625 * (t - B3) * (t - B3) + .75)
if (t < B4): return 1 - (7.5625 * (t - B5) * (t - B5) + .9375)
return 1 - (7.5625 * (t - B6) * (t - B6) + .984375)
func bounce_out(t:float) -> float:
if (t < B1): return 7.5625 * t * t
if (t < B2): return 7.5625 * (t - B3) * (t - B3) + .75
if (t < B4): return 7.5625 * (t - B5) * (t - B5) + .9375
return 7.5625 * (t - B6) * (t - B6) + .984375
func bounce_in_out(t:float) -> float:
if (t < .5):
t = 1 - t * 2
if (t < B1): return (1 - 7.5625 * t * t) / 2
if (t < B2): return (1 - (7.5625 * (t - B3) * (t - B3) + .75)) / 2
if (t < B4): return (1 - (7.5625 * (t - B5) * (t - B5) + .9375)) / 2
return (1 - (7.5625 * (t - B6) * (t - B6) + .984375)) / 2
else:
t = t * 2 - 1
if (t < B1): return (7.5625 * t * t) / 2 + .5
if (t < B2): return (7.5625 * (t - B3) * (t - B3) + .75) / 2 + .5
if (t < B4): return (7.5625 * (t - B5) * (t - B5) + .9375) / 2 + .5
return (7.5625 * (t - B6) * (t - B6) + .984375) / 2 + .5
# 円
func circ_in(t:float) -> float:
return -(sqrt(1 - t * t) - 1)
func circ_out(t:float) -> float:
return sqrt(1 - (t - 1) * (t - 1))
func circ_in_out(t:float) -> float:
if t <= .5:
return (sqrt(1 - t * t * 4) - 1) / -2
else:
return (sqrt(1 - (t * 2 - 2) * (t * 2 - 2)) + 1) / 2
# 指数関数
func expo_in(t:float) -> float:
return pow(2, 10 * (t - 1))
func expo_out(t:float) -> float:
return -pow(2, -10*t) + 1
func expo_in_out(t:float) -> float:
if t < .5:
return pow(2, 10 * (t * 2 - 1)) / 2
else:
return (-pow(2, -10 * (t * 2 - 1)) + 2) / 2
# バック
func back_in(t:float) -> float:
return t * t * (2.70158 * t - 1.70158)
func back_out(t:float) -> float:
return 1 - (t - 1) * (t-1) * (-2.70158 * (t-1) - 1.70158)
func back_in_out(t:float) -> float:
t *= 2
if (t < 1):
return t * t * (2.70158 * t - 1.70158) / 2
else:
t -= 1
return (1 - (t - 1) * (t - 1) * (-2.70158 * (t - 1) - 1.70158)) / 2 + .5
# 弾力関数
const ELASTIC_AMPLITUDE = 1.0
const ELASTIC_PERIOD = 0.4
func elastic_in(t:float) -> float:
t -= 1
return -(ELASTIC_AMPLITUDE * pow(2, 10 * t) * sin( (t - (ELASTIC_PERIOD / (2 * PI) * asin(1 / ELASTIC_AMPLITUDE))) * (2 * PI) / ELASTIC_PERIOD))
func elastic_out(t:float) -> float:
return (ELASTIC_AMPLITUDE * pow(2, -10 * t) * sin((t - (ELASTIC_PERIOD / (2 * PI) * asin(1 / ELASTIC_AMPLITUDE))) * (2 * PI) / ELASTIC_PERIOD) + 1)
func elastic_in_out(t:float) -> float:
if (t < 0.5):
t -= 0.5
return -0.5 * (pow(2, 10 * t) * sin((t - (ELASTIC_PERIOD / 4)) * (2 * PI) / ELASTIC_PERIOD))
else:
t -= 0.5
return pow(2, -10 * t) * sin((t - (ELASTIC_PERIOD / 4)) * (2 * PI) / ELASTIC_PERIOD) * 0.5 + 1
func exec(type:int, t:float) -> float:
var function = get_function(type)
return function.call(t)
# @param v 0.0〜1.0
func step(type:int, start:float, end:float, v:float) -> float:
if start == end:
return start # 開始と終了が同じ
var a = start
var b = end
if v <= 0.0:
# 開始より小さい
return start
if v >= 1.0:
# 終了より大きい
return end
var d = b - a
var t = v
var func_name = get_function(type)
return a + (d * call(func_name, t))
func get_function(type:int) -> String:
var tbl = {
eType.LINEAR: "linear", # 線形
eType.QUAD_IN: "quad_in", # 二次関数
eType.QUAD_OUT: "quad_out",
eType.QUAD_INOUT: "quad_in_out",
eType.CUBE_IN: "cube_in", # 三次関数
eType.CUBE_OUT: "cube_out",
eType.CUBE_INOUT: "cube_in_out",
eType.QUART_IN: "quart_in", # 四次関数
eType.QUART_OUT: "quart_out",
eType.QUART_INOUT: "quart_in_out",
eType.QUINT_IN: "quint_in", # 五次関数
eType.QUINT_OUT: "quint_out",
eType.QUINT_INOUT: "quint_in_out",
eType.SMOOTH_STEP_IN: "smooth_step_in", # スムーズ曲線
eType.SMOOTH_STEP_OUT: "smooth_step_out",
eType.SMOOTH_STEP_INOUT: "smooth_step_in_out",
eType.SMOOTHER_STEP_IN: "smoother_step_in", # よりスムーズな曲線
eType.SMOOTHER_STEP_OUT: "smoother_step_out",
eType.SMOOTHER_STEP_INOUT: "smoother_step_in_out",
eType.SIN_IN: "sine_in", # SIN関数
eType.SIN_OUT: "sine_out",
eType.SIN_INOUT: "sine_in_out",
eType.BOUNCE_IN: "bounce_in", # バウンス
eType.BOUNCE_OUT: "bounce_out",
eType.BOUNCE_INOUT: "bounce_in_out",
eType.CIRC_IN: "circ_in", # サークル
eType.CIRC_OUT: "circ_out",
eType.CIRC_INOUT: "circ_in_out",
eType.EXPO_IN: "expo_in", # 指数関数
eType.EXPO_OUT: "expo_out",
eType.EXPO_INOUT: "expo_in_out",
eType.BACK_IN: "back_in", # バック
eType.BACK_OUT: "back_out",
eType.BACK_INOUT: "back_inout",
eType.ELASTIC_IN: "elastic_in", # 弾力関数
eType.ELASTIC_OUT: "elastic_out",
eType.ELASTIC_INOUT: "elastic_in_out",
}
if tbl.has(type):
return tbl[type]
else:
print("未定義のイージング関数: %d"%type)
return "linear"
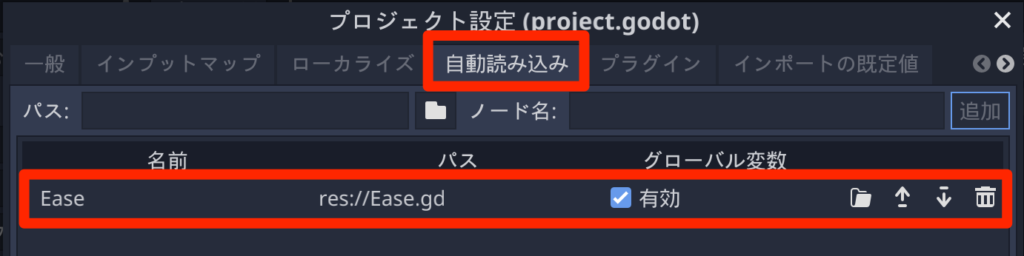
そうしたら、プロジェクトの設定 > 自動読み込みから「Ease.gd」を自動読み込み有効にしておきます。
実装サンプルコード
例えば以下のように使います
extends Node2D
var timer = 0.0
onready var icon = $Icon
onready var icon2 = $Icon2
func _process(delta: float) -> void:
if Input.is_action_just_pressed("ui_accept"):
timer = 0
if timer < 3.0:
timer += delta
var t = timer / 3.0 # 0.0〜1.0に変換
# そのままイージング関数を使う場合
icon.position.x = 200 + 600 * Ease.expo_out(t)
icon.position.y = 200;
# step()で開始と終端を指定する
icon2.position.x = Ease.step(Easing.eType.BOUNCE_OUT, 200, 800, t)
icon2.position.y = 300変化量だけ欲しい場合には、Ease.###_in/out() を使い、
開始地点と終端から位置を求めたい場合には Ease.step() を使用します。

なおイージング関数の種類についてはこちらのサイトが詳しいと思います。
完成プロジェクト
今回作成したプロジェクトを添付しておきます。