多関節を実現する方法は、
- CCD法
- インバースキネマティクス(IK)
などの方法があるみたいです。
シューティングゲームアルゴリズムマニアックス(Cmagazine)にIKでの実装方法がのっていたので、その実装方法の紹介となります。
目次
インバースキネマティクスとは?
末端部分の位置を先に決めて、
その関節の末端位置を実現するための親となる関節の角度を
簡易的に逆計算する手法
Wikipediaより
多関節の目的
例えば、触手みたいなものを作るとします。
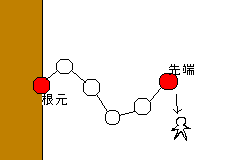
丸いのを関節とします。「根元」は壁に固定されています。
で、やりたいのは、「先端」をプレイヤーめがけて移動させる方法です。
ここで、「先端」をそのままプレイヤーに移動させてしまうと、関節と関節の間の距離が離れてしまいます。まあ、触手であれば、それでもいいのですが、これが人間(か何かの生物)の場合、不自然に腕が伸びてしまい、リアリティがなくなってしまいます。
つまり、
- 関節と関節との「距離を固定」したままで、目標めがけて移動する
のが多関節の目的です。
IKの処理手順
- 「先端」から「根元」に向かって、
- 「先端」の位置を動かしながら、
- 各関節の「角度」を決める。
- 1-2によって決まった角度を元に、「根元」から「先端」に向かって、各関節の「座標」を求める。
というのが大まかな手順となります。
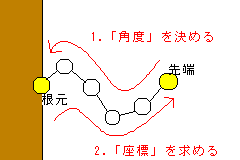
1は、「先端から回転させる」ということです。
ここでは「根元から回転させてもいいのでは……?」と思ったかもしれません。
ですが、例えば、机にあるリンゴを取る動きを考えたとき、
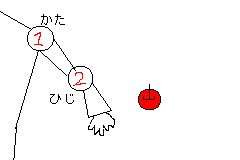
人は、①の関節を回してリンゴを取ろうとするよりも、まずは②の関節を回してリンゴを取ります。そのほうが運動量が少なくて済むからです。(②の回転のみで届かない(回転角度の限界を超えたなど)場合に、①を回転します)
つまり、自然な動きをするためには「先端」から回す必要があります。(※注:このあたりやや推測です。どうやら計算の負荷を低くするためらしいです)
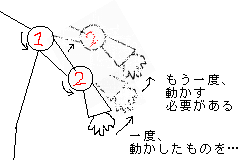
2は、「根元から座標を決めていく」ということです。各関節の「角度」が決まった際、「先端」から座標を決めると、各関節よりも先端の方にある関節の座標を再計算する必要が出てくるからです。
角度を決める
先端にある関節の方から、「先端」を除いた全ての関節について「角度」を求めます。
と、その前に、念のために……。
関節の「角度」というのは、根元に近い関節との角度に対する相対的なものです。
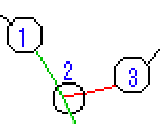
2の関節の角度とは、1と2を結んだ線(緑色)と、2と3を結んだ線(赤色)からなる角度のことです。
回す方向の候補は3つあります。
- 回らない
- 右に回す
- 左に回す
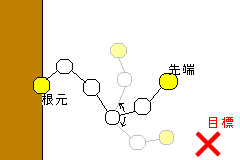
これら3つの操作によって、「先端」が最も目標に近くなるものを選択します。
で、計算ですが、真面目に座標を回転させて、距離を求めて、、というやり方でもいいのですが、内積を使うと簡単に決めることができます。
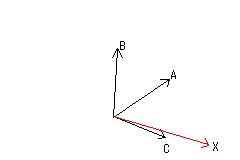
まず、関節から目標へのベクトルを求めます。(赤い線)
これをXベクトルとします。
次に、関節から先端へのベクトルを求めます。
「回らない」「右に回す」「左に回す」それぞれのベクトルをA・B・Cベクトルとします。(※「回らない」のベクトルを求めれば、回転行列をかけることにより、ベクトルを回転できます)
そして、A・B・CベクトルとベクトルXとの内積をそれぞれ求めて、最も値が大きい(作られる角度が小さい)操作が、目標に一番近いものとなります。
そして、、、ここが大きなポイントですが、決まった角度を元に、「先端」だけ動かしてしまいます。この時点では、関節は角度だけ決めて動かさずに、「先端」だけは動かしてしまいます。
そんな感じで、先端にある関節の方から、「先端」の座標を動かして、その座標を基準に、根元にある関節からみて、より目標に近い方へ回転して、また「先端」の座標を動かす、、、という作業を繰り返して、それぞれの回転角度を決めていきます。
関節の座標を決める
関節の角度が全て決まったら、それに基づいて、関節の「座標」を求めます。まあ、これは簡単で、単純に直前(「根元」に近い側)の関節の座標と角度から、自身の座標を決定するだけです。
ソースコード
D言語で実装すると、こんな感じです。
/**
* 多関節ノード
*/
class Node
{
public:
float x; // 座標(X)
float y; // 座標(Y)
float rad; // 回転角度
this(float x=0, float y=0, float rad=0)
{
this.x = x;
this.y = y;
this.rad = rad;
}
}
/**
* 多関節用ベクトル
*/
struct JointVector
{
float x; // X成分
float y; // Y成分
float n; // 内積の結果
/**
* 内積を求めて結果を保持する
*/
void dot(float dx, float dy)
{
n = x*dx + y*dy;
}
}
/**
* 関節の移動(Inverse Kinematics)
* @param nodes 関節([0]根元~[$-1]先端)
* @param vRad 関節の回転角度
* @param lRad 回転角度の限界値
* @param distance 関節間の距離
* @param x 目標座標(X)
* @param y 目標座標(Y)
*/
void MoveJoints(Node[] nodes, float vRad, float lRad,
float distance, float x, float y)
{
{
float cos = Hell_cos(vRad);
float sin = Hell_sin(vRad);
// 前半の処理(回転角度を求める)
Node nTip = nodes[$ - 1]; // 先端ノード
// 先端⇒根元
// リバースイテレート。先端ノードは処理しない
for(int i = nodes.length - 1; i >= 0; i--)
{
Node n = nodes[i];
// 関節から自機へのベクトルの計算
float dx = x - n.x;
float dy = y - n.y;
// 関節から先端へのベクトルと内積の計算
JointVector jNode;
jNode.x = nTip.x - n.x;
jNode.y = nTip.y - n.y;
jNode.dot(dx, dy);
// 右回りのベクトルの計算
JointVector jRight;
if(n.rad + vRad <= lRad)
{
jRight.x = cos*jNode.x - sin*jNode.y;
jRight.y = sin*jNode.x + cos*jNode.y;
jRight.dot(dx, dy);
}
else
{
// 限界を超えたので回せない
jRight.n = jNode.n;
}
// 左回りのベクトルの計算
JointVector jLeft;
if(n.rad - vRad >= -lRad)
{
jLeft.x = cos*jNode.x + sin*jNode.y;
jLeft.y = -sin*jNode.x + cos*jNode.y;
jLeft.dot(dx, dy);
}
else
{
// 限界を超えたので回せない
jLeft.n = jNode.n;
}
// 回転方向の選択
// 内積を比較して、回転を3通りのなかから選ぶ
// 先端を回転させて、新しい先端の位置を求める
if(jRight.n > jNode.n && jRight.n > jLeft.n)
{
// 右回り
n.rad += vRad;
nTip.x = n.x + jRight.x;
nTip.y = n.y + jRight.y;
}
if(jLeft.n > jNode.n && jLeft.n > jRight.n)
{
// 左回り
n.rad -= vRad;
nTip.x = n.x + jLeft.x;
nTip.y = n.y + jLeft.y;
}
}
}
// 後半の処理(座標を決める)
float px = distance;
float py = 0;
// 根元⇒先端
// 根元は移動しない
for(int i = 1; i < nodes.length; i++)
{
Node n1 = nodes[i-1];
Node n2 = nodes[i];
float cos = Hell_cos(n1.rad);
float sin = Hell_sin(n1.rad);
float dx = cos*px - sin*py;
float dy = sin*px + cos*py;
n2.x = n1.x + dx;
n2.y = n1.y + dy;
px = dx;
py = dy;
}
}(Hell_sin()/Hell_cos()は、それぞれmathライブラリのsin/cosと同じです)

