目次
1.はじめに
ここでは、 Grid-based (グリッド制) の戦術SLGの作り方について説明をします。
戦術SLGとは、将棋やチェスのように、自分のコマを動かして相手のコマを倒すゲームのことです。将棋やチェスと違うのは、コマに色々なパラメータがあることです。例えば「ファイヤーエンブレム」や「オウガバトル」のようなゲームで必要とされる処理となります。
今回の記事はここを参考にしました。
なかなか詳しく書いてあるので、勉強になります。
普通の戦術SLGでは、コマを選択したときに、どこまで移動できるのかを明るくしたりして、視覚的に分かるようにしています。今回は、その移動範囲の求め方を説明します。
2.基本編
まず最初は、
- 「10×10」のマップ
- 地形のタイプは「平地」(移動力を「1」消費する)しか存在しない
- コマの初期位置は(x, y) = (6, 6)
- コマの移動力は「3」
といったシンプルなモデルで考えてみます。
地形データを作成する
「10×10」のマップなので、そのままですが、「10×10」の配列を作成します。
配列の初期値として、「-1」を設定します。

移動データを作成する
コマの初期位置と移動力を設定します。初期位置は(6, 6)、移動力は「3」とします。
移動範囲を求める
データの準備ができたので、移動範囲を求めます。初期処理として、開始位置に移動力を指定します。

ここで2つ関数を作成します。
一つは現在位置から、上/下/左/右を探索する関数です。この関数を「Search4」とします。
もう一つは移動先が移動可能な場所であるかを判定する関数です。この関数を「Search」とします。
「Search4」は各方向(上/下/左/右)ごとに、探索する地点の座標と移動力を「Search」に渡します。「Search」は移動力を1つ減らし、移動力が残っていれば、「Search4」を再帰呼び出しします。
たとえば、「Search4」で上を探索すると、「Search」で「2」を設定します。

移動力がまだ残っていますので、「Search4」を再帰呼び出しし、上を探索して、「Search」で「1」を設定します。

さらに、移動力がまだ残っていますので、「Search4」を再帰呼び出しし、上を探索して、「Search」で「0」を設定します。

移動力がなくなったので、(6, 4)地点に戻り、下を探索し、「Search」で「0」を設定します。
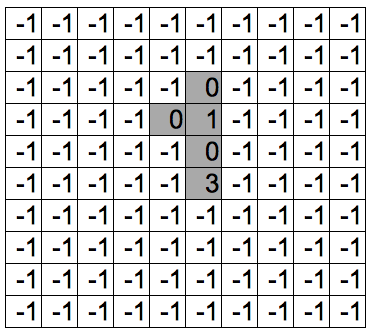
移動力がなくなったので、(6, 4)地点に戻り、右を探索し、「Search」で「0」を設定します。

といったことを繰り返すと、以下のようになります。
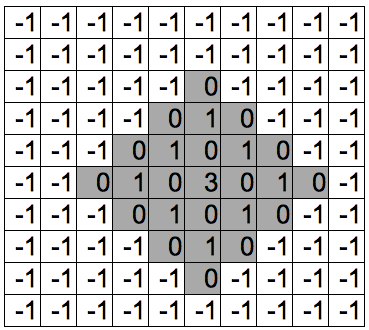
実は、この処理は無駄なことをしています。例えば、上・上と探索した後に上・下と探索していたりします。移動力が大きいほど、探索範囲は大きくなりますので、環境によっては処理速度が問題となることもあり得ます。
そこで、「Search」関数で、「移動力-1 < 地形の値」であった場合には、その地点の探索を行わないようにします。こうすることで無駄な処理がなくなり、以下のようになると思います。
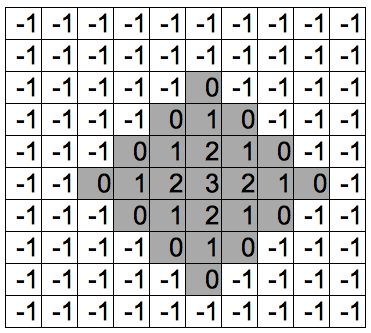
これで移動範囲を求めることができました。
3.応用編
応用として、以下の地形データを追加し、バリエーションを持たせます。
- 「森」:移動力を「2」消費する
- 「山」:移動不可
地形データを作成する
マップデータを以下のようにしてみます。

ところどころにある、「-2」が「森」、「-9」が「山」です。
移動できないはずなのに、なぜ「山」が「-9」であるのかというと、現在の移動力が「3」であるため、実質的に移動不可となるためです。作ってみるとわかりますが、例外的な処理をもうけて処理を複雑にするよりは、こうしたほうが処理が楽になります。(もちろん移動量が9以上になる場合は「-100」とかにしておく必要があります)
移動範囲を求める
移動範囲の求め方は、基本編とほぼ変わりません。違うのは、「Search」関数で単純に移動力を「-1」としていたものを、地形の値から引くというところです。
具体的には、以下のようになります。
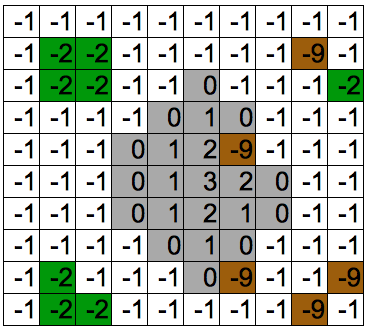
どうでしょうか。それっぽくなったのではないでしょうか。
今回の処理は、単に移動範囲を求めるだけでなく、魔法や飛び道具などの射程範囲・効果範囲や、コンピュータの索敵範囲を求めるのに使える基本的な処理となります。
関連記事
移動範囲に対して、最短距離を求めるアルゴリズムである「A*」の実装方法については以下の記事に書きました
 A-starアルゴリズム
A-starアルゴリズム 
