この記事では Curve2D を使用したベジェ曲線の作り方を解説します。
目次
ベジェ曲線とは
そもそもベジェ曲線とはどういうものなのかを説明します。
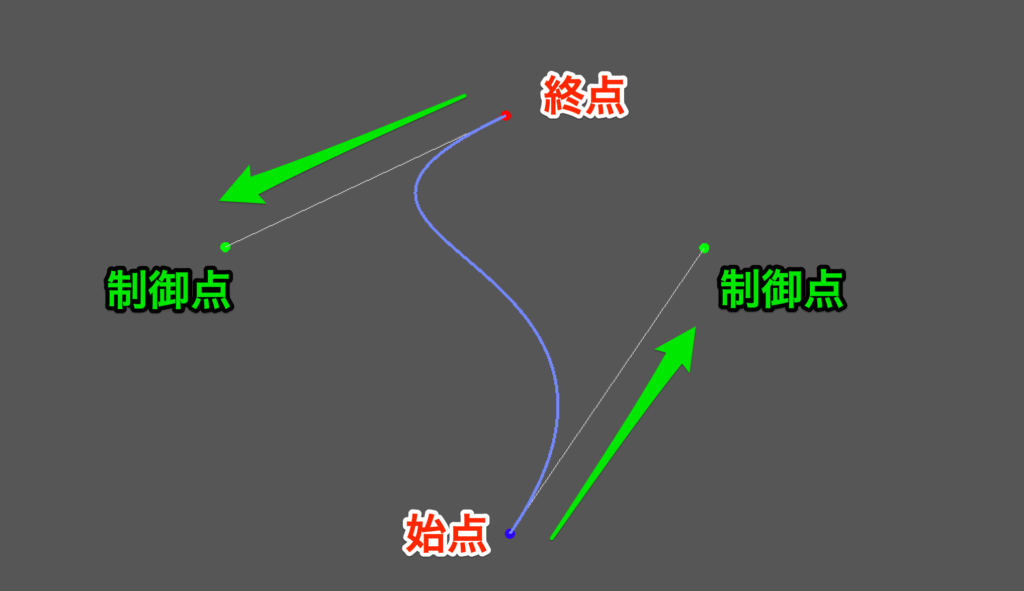
ベジェ曲線とは、「始点」から「終点」に向けて制御点に引っ張られるようにして作られる曲線となります。
他によく知られている曲線としては「エルミート曲線」「Bスプライン曲線」などがありますが、ベジェ曲線はカーブの作られ方が比較的わかりやすいため、使い勝手が良いです。
Godotでのベジェ曲線の作り方
べジェ曲線を実装するには、やや数学の知識が必要となるのですが、Godotでは Curve2D というクラスが存在しており、これを使用すると簡単にべジェ曲線が作れます。
以下、Godotでのサンプルコードです。
onready var line = $Line2D # Line2D
var curve = Curve2D.new() # Curve2Dを生成
# ベジェ曲線を生成
func _create_curve():
# 制御点 (方向ベクトル) を求める
var c0 = $P1.position - $P0.position # 始点の制御点
var c1 = $P3.position - $P2.position # 終点の制御点
curve.bake_interval = 2.0 # 分割距離 (小さいほど細かくなる)
# 始点と制御点を設定 (outに制御点を指定する)
curve.add_point($P0.position, Vector2.ZERO, c0)
# 終点と制御点を設定 (inに制御点を指定する)
curve.add_point($P2.position, c1, Vector2.ZERO)
# Line2Dにポイントを設定する
line.clear_points()
for p in curve.get_baked_points():
line.add_point(p)
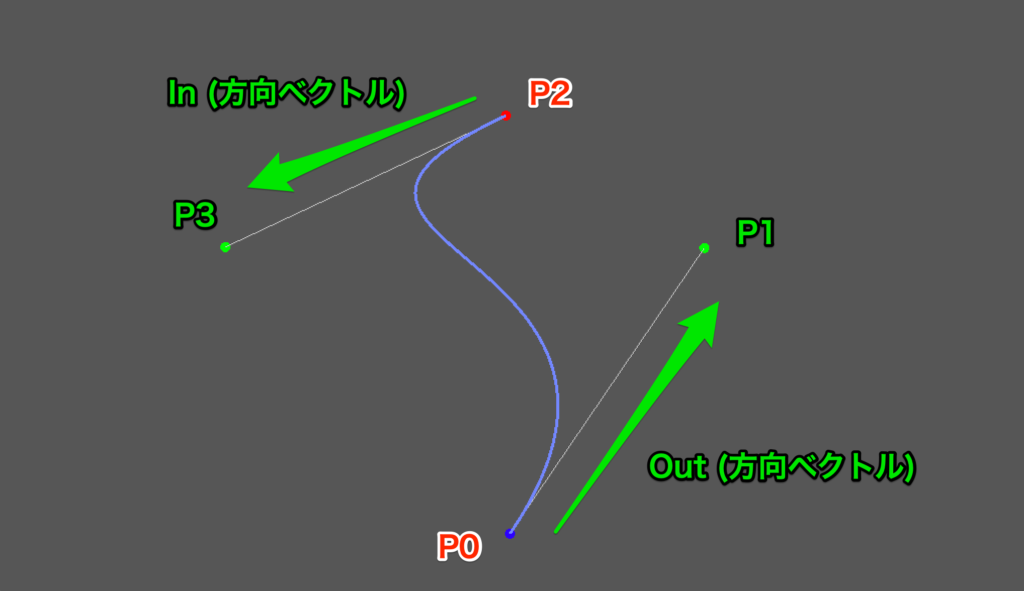
- P0: 始点
- P1: 始点の制御点
- P2: 終点
- P3: 終点の制御点
まずは制御点ですが、方向ベクトルとして渡す必要があります。
# 制御点 (方向ベクトル) を求める
var c0 = $P1.position - $P0.position # 始点の制御点
var c1 = $P3.position - $P2.position # 終点の制御点そのため、この部分で位置ベクトルを減算して、方向ベクトルを求めています。
次に、Curve2D.add_point() には、最初の引数には “座標” を渡し、2番目・3番目の引数には先ほど計算した制御点(正確には方向ベクトル)を渡しています。
# 始点と制御点を設定 (outに制御点を指定する)
curve.add_point($P0.position, Vector2.ZERO, c0)
# 終点と制御点を設定 (inに制御点を指定する)
curve.add_point($P2.position, c1, Vector2.ZERO)始点は、線が出ていく点なので、3番目の引数のみ制御点を渡します。
終点は、線が入る点なので、2番目の引数のみ制御点を渡しています。
実際に作られる曲線は、Curve2D.bake_interval で作られる点の細かさを指定します。
curve.bake_interval = 2.0 # 分割距離 (小さいほど細かくなる)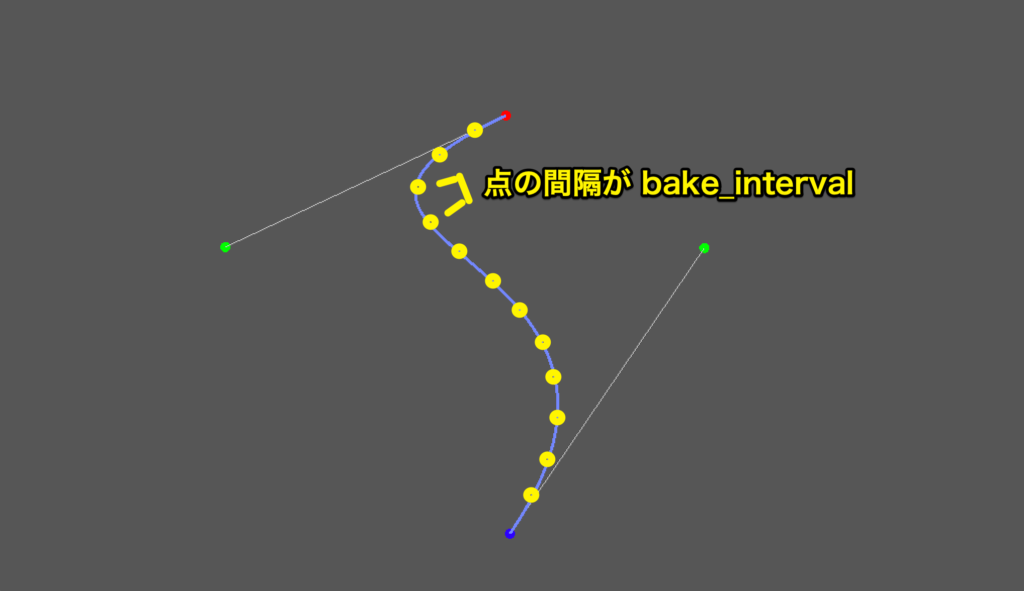
曲線はなんとなく自動で滑らかにしてくれるイメージがあるかもしれませんが、実際には上記の図のように、細かく分割された点を直線でつなぐことで作られます。
その点の距離の間隔が “Curve2D.bake_interval” となり、この値を小さくするほど滑らかな曲線にすることができます。
Curve2Dを使った曲線移動の実装例
作成されたベジェ曲線のポイントは Curve2D.get_baked_points() を使用すると取得できます。
以下は時間経過に合わせてベジェ曲線上に移動するサンプルとなります。
onready var line = $Line2D
onready var icon = $Icon
var timer = 0
var curve = Curve2D.new()
func _process(delta):
timer += delta
var max_points = curve.get_baked_points().size()
# 3.0秒で終端に移動するようにする
var rate = timer / 3.0
if rate < 1.0:
var idx = (max_points * rate)
icon.position = curve.get_baked_points()[idx]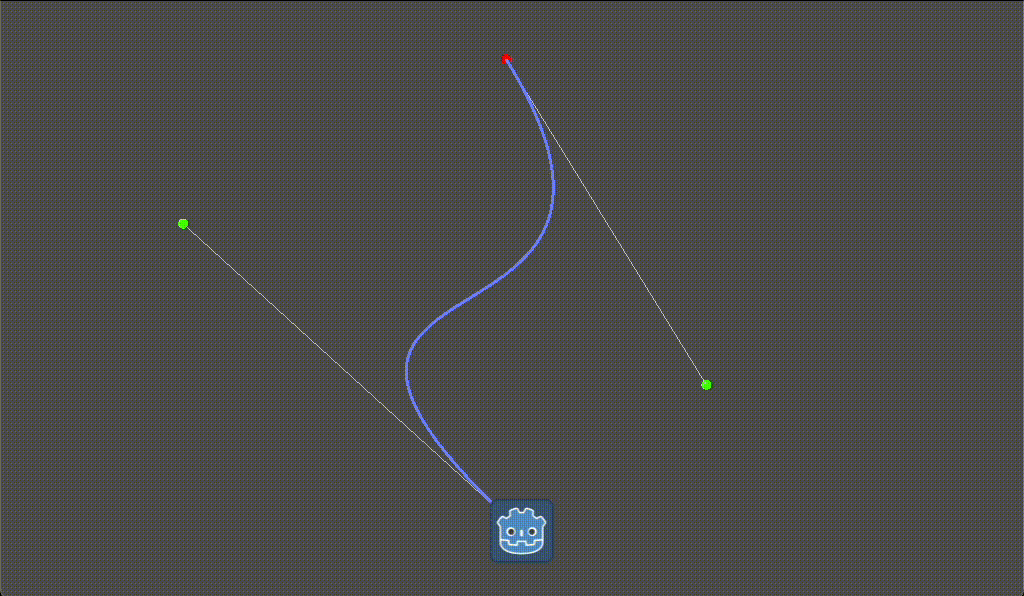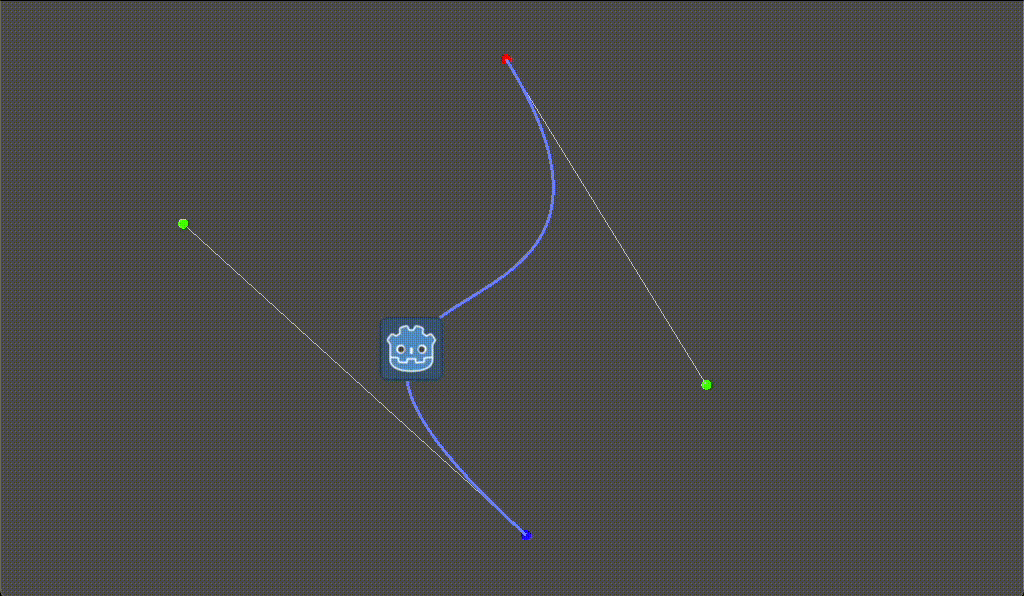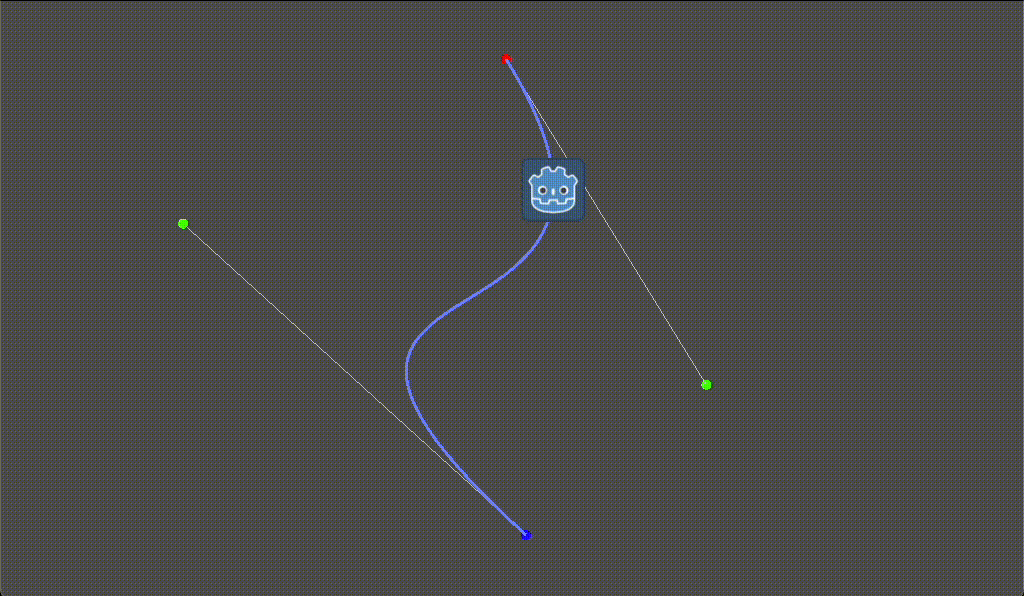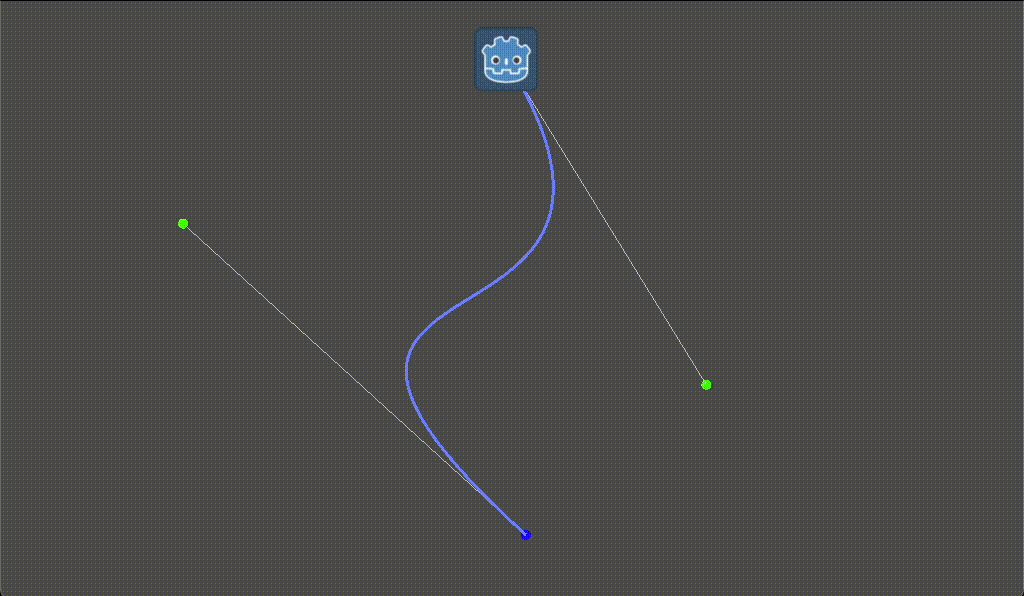
サンプルプロジェクト
今回作成したプロジェクトファイルは以下からダウンロードできます。