目次
曲線を使うメリット
例えば、放物線を描いて動く敵を作るとします。その場合に、
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| y | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
という座標のパターンを持つとします。
そのとき、この敵の移動を直接数値で保持すると以下のようなテーブルが必要となります。
x,y
----------
move 0,16
move 1,9
move 2,4
move 3,1
move 4,0
move 5,1
move 6,4
move 7,9
move 8,16となります。
これはこれで細かく動きを制御できていいのですが、この座標のデータを作るのが大変ですよね。
そこで、曲線の式を使います。この例でしたら、
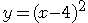
となります。
この式により、滑らかな曲線の動きを作ることができます。さらに、入力変数となるxが実数であった場合にも、こまかく動きを制御できますね。
エルミート曲線
ただ、
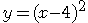
という式で表現できる動きには限界があります。
そこでエルミート曲線という3次元の曲線の式を使うと、始点と終点を指定してその間を補間する曲線を作ることができます。
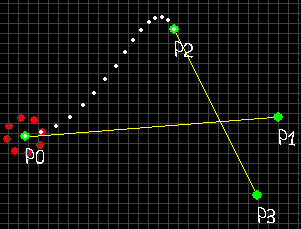
エルミート曲線のパラメータは以下のようになります。
- 始点(P0)
- 始点の法線(P1)
- 終点(P2)
- 終点の法線(P3)
この場合の法線とは、各点から線を引こうとする力のようなものです。これにより図のような美しい曲線を描くことができます。
では、エルミート曲線の式の考え方を紹介します。
エルミート曲線のもととなるのが、基本的な3次曲線で、未知数をa,b,c,d、入力変数をuとすると、
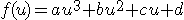
入力変数uが 0~1.0 の範囲で動くとします。そうすると、u=0は始点で、u=1は終点となり、始点は
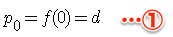
終点は、
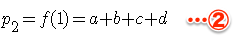
となります。
次に法線です。この場合の法線は曲線の接線ですので、f(u)を微分することにより求めることができます。
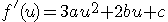
よって、始点の法線は
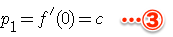
終点の法線は
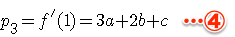
となります。
①と③を②に代入して
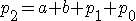
③を④に代入して
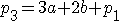
この方程式をa,bについて解くと、
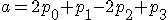
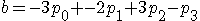
となり、求める式は、
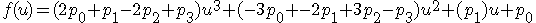
となります。
以下、C++でのエルミート曲線を元に座標のリストを生成するサンプルコードです。
/**
* 2次元ベクトル構造体
*/
struct Vec2D
{
float x, y;
Vec2D(float x, float y)
{
this->x = x;
this->y = y;
}
};
#include <vector>
using namespace std;
/**
* エルミート曲線の座標リストを取得
* @param p0 始点
* @param v0 始点ベクトル
* @param p1 終点
* @param v1 終点ベクトル
* @param DIVIDE 分解度
* @return 座標リスト
*/
vector<Vec2D> getHermiteCurvePointList(
Vec2D *p0, Vec2D *v0,
Vec2D *p1, Vec2D *v1,
int DIVIDE=16)
{
vector<Vec2D> pList;
for(int i = 0; i < DIVIDE; i++)
{
float u1 = i*1.0/(DIVIDE-1);
float u2 = u1*u1;
float u3 = u1*u1*u1;
float mP0 = 2*u3 - 3*u2 + 0 + 1;
float mV0 = u3 - 2*u2 + u1;
float mP1 = -2*u3 + 3*u2;
float mV1 = u3 - u2;
pList.push_back(
Vec2D(
p0->x*mP0 + v0->x*mV0 + p1->x*mP1 + v1->x*mV1,
p0->y*mP0 + v0->y*mV0 + p1->y*mP1 + v1->y*mV1));
}
return pList;
}引数の「DIVIDE」で、曲線の分割数を増やすことができます。
ベジェ曲線
ただ、エルミート曲線だと、例えばトラックが旋回するような起動となり、ダイナミックな曲線を作ることができません。そこで、曲線の生成にもうすこし柔軟性を持たせたのがベジェ曲線です。
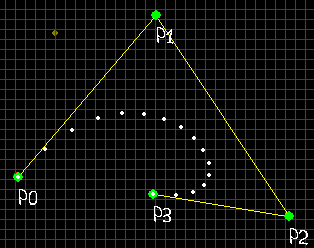
ベジェ曲線では、以下のパラメータを持ちます。
- 始点(P0)
- 制御点1(P1)
- 制御点2(P2)
- 終点(P3)
法線ではなくて、制御点により曲線を求めます。制御点は何をするのかというと、始点や終点との線分を求めるのに利用されます。そして、その線分を「内分」するのがベジェ曲線です。
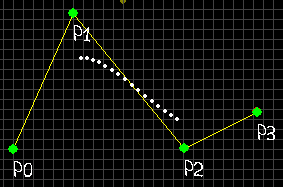
では、式を2次曲線に簡略化した図を見てみます。
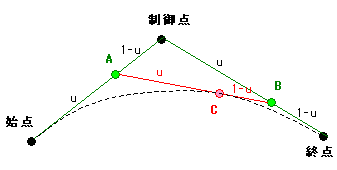
エルミート曲線と同じく、uを0~1.0の範囲で動かしています。始点をP0、制御点をP1、終点をP2とします。
手順としては、まず、始点と制御点との線分をuと1-uで内分します。(点A)
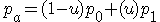
また、制御点と終点との線分をuと1-uで内分します。(点B)
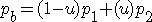
そして、点Aと点Bとの線分をuと1-uで内分することにより、曲線を求めることができます。(点C)
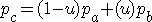
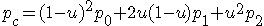
という感じです。制御点を2つにする場合は、さらにこの点を内分して、制御点を3つにする場合には、さらにさらに内分して、、、という手順を踏むことになります。
ということで、ひとまず制御点が2つの場合のC++のサンプルです。
/**
* 2次元ベクトル構造体
*/
struct Vec2D
{
float x, y;
Vec2D(float x, float y)
{
this->x = x;
this->y = y;
}
};
#include <vector>
using namespace std;
/**
* ベジェ曲線の座標リストを取得
* @param p0 始点
* @param p1 制御点1
* @param p2 制御点2
* @param p3 終点
* @param DIVIDE 分解度
* @return 座標リスト
*/
vector<Vec2D> getBezierCurvePointList(
Vec2D *p0, Vec2D *p1,
Vec2D *p2, Vec2D *p3,
int DIVIDE=16)
{
vector<Vec2D> pList;
for(int i = 0; i < DIVIDE; i++)
{
float u = i*1.0/(DIVIDE-1);
float mP0 = (1-u)*(1-u)*(1-u);
float mP1 = 3 * u * (1-u)*(1-u);
float mP2 = 3 * u*u * (1-u);
float mP3 = u*u*u;
pList.push_back(
Vec2D(
p0->x*mP0 + p1->x*mP1 + p2->x*mP2 + p3->x*mP3,
p0->y*mP0 + p1->y*mP1 + p2->y*mP2 + p3->y*mP3));
}
return pList;
}Bスプライン曲線
実はベジェ曲線では、制御点を増やしていくとある問題が発生します。それは、
- 折れ曲がってしまう(キレイな曲線でなくなる)
ということです。それを解決したのがBスプライン曲線です。
…ただ、Bスプライン曲線は、始点と終点の位置が直感的でないので使い方が難しく、あまり使うことはないかもしれません
以下、Bスプライン曲線を実装したコードです。
/**
* 2次元ベクトル構造体
*/
struct Vec2D
{
float x, y;
Vec2D(float x, float y)
{
this->x = x;
this->y = y;
}
};
#include <vector>
using namespace std;
/**
* Bスプライン曲線の座標リストを取得
* @param p0 始点
* @param p1 制御点1
* @param p2 制御点2
* @param p3 終点
* @param DIVIDE 分解度
* @return 座標リスト
*/
vector<Vec2D> getBSplineCurvePointList(
Vec2D *p0, Vec2D *p1,
Vec2D *p2, Vec2D *p3,
int DIVIDE=16)
{
vector<Vec2D> pList;
for(int i = 0; i < DIVIDE; i++)
{
float u1 = i*1.0/(DIVIDE-1);
float u2 = u1*u1;
float u3 = u1*u1*u1;
float mP0 = (-1*u3 + 3*u2 - 3*u1 + 1)*1.0 / 6;
float mP1 = ( 3*u3 - 6*u2 + 4)*1.0 / 6;
float mP2 = (-3*u3 + 3*u2 + 3*u1 + 1)*1.0 / 6;
float mP3 = ( 1*u3 )*1.0 / 6;
pList.push_back(
Vec2D(
p0->x*mP0 + p1->x*mP1 + p2->x*mP2 + p3->x*mP3,
p0->y*mP0 + p1->y*mP1 + p2->y*mP2 + p3->y*mP3));
}
return pList;
}
